题目内容
4.解不等式组:$\left\{\begin{array}{l}{\frac{x-2}{5}<0}\\{2(2x-5)≤3(4x+2)}\end{array}\right.$并写出该不等式组的整数解.分析 分别求出不等式组中两不等式的解集,找出解集的公共部分,确定出不等式组的整数解即可.
解答 解:$\left\{\begin{array}{l}{\frac{x-2}{5}<0①}\\{2(2x-5)≤3(4x+2)②}\end{array}\right.$,
由①得:x<2;
由②得:x≥-2,
∴不等式组的解集为-2≤x<2,
则不等式组的整数解为-2,-1,0,1.
点评 此题考查了解一元一次不等式组,以及一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
15.为了了解某校八年级600名学生的体重情况,从中抽出了50名学生的体重数据进行统计分析,在这个问题中,样本是( )
| A. | 600学生 | B. | 被抽取的50名学生 | ||
| C. | 600学生的体重 | D. | 被抽取的50名学生的体重 |
12.从长为4cm,7cm,9cm,11cm的四条线段中任选三条线段,不能组成一个三角形的为( )
| A. | 4cm,7cm,9cm | B. | 4cm,7cm,11cm | C. | 4cm,9cm,11cm | D. | 7cm,9cm,11cm |
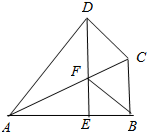 如图,四边形ABCD是筝形,且AB=8,BC=4,∠ABC=90°,过D作DE⊥AB交AC于点F,连接BF.求证:DF=CD,并判断四边形BCDF的形状.
如图,四边形ABCD是筝形,且AB=8,BC=4,∠ABC=90°,过D作DE⊥AB交AC于点F,连接BF.求证:DF=CD,并判断四边形BCDF的形状.