题目内容
 已知:如图,五边形ABCDE是正五边形,连接BD、CE,交于点P. 求证:四边形ABPE是平行四边形.
已知:如图,五边形ABCDE是正五边形,连接BD、CE,交于点P. 求证:四边形ABPE是平行四边形.考点:平行四边形的判定
专题:证明题
分析:首先根据正五边形的性质可得正五边形的每个内角的度数是
=108°,AB=BC=CD=DE=AE,然后再证明∠A=∠P,∠ABP=∠AEP可根据两组对角分别相等的四边形是平行四边形可得结论.
| (5-2)×180° |
| 5 |
解答:证明:∵五边形ABCDE是正五边形,
∴正五边形的每个内角的度数是
=108°,
AB=BC=CD=DE=AE,
∴∠DEC=∠DCE=
×(180°-108°)=36°,
同理∠CBD=∠CDB=36°,
∴∠ABP=∠AEP=108°-36°=72°,
∴∠BPE=360°-108°-72°-72°=108°=∠A,
∴四边形ABPE是平行四边形.
∴正五边形的每个内角的度数是
| (5-2)×180° |
| 5 |
AB=BC=CD=DE=AE,
∴∠DEC=∠DCE=
| 1 |
| 2 |
同理∠CBD=∠CDB=36°,
∴∠ABP=∠AEP=108°-36°=72°,
∴∠BPE=360°-108°-72°-72°=108°=∠A,
∴四边形ABPE是平行四边形.
点评:此题主要考查了平行四边形的判定,以及正五边形的性质,关键是掌握两组对角分别相等的四边形是平行四边形.

练习册系列答案
相关题目
如果a、b是方程x2-3x+1=0的两根,那么代数式a2+2b2-3b的值为( )
| A、6 | B、-6 | C、7 | D、-7 |
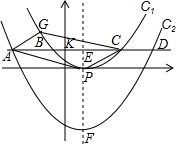 已知顶点为P的抛物线C1的解析式是y=a(x-3)2(a≠0),且经过点(0,1).
已知顶点为P的抛物线C1的解析式是y=a(x-3)2(a≠0),且经过点(0,1).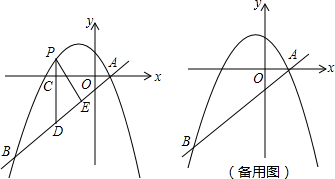
 已知△ABC,
已知△ABC, 如图,某登山队在山脚A处测得山顶B处的仰角为45°,沿坡角30°的斜坡AD前进1000m后到达D处,又测得山顶B处的仰角为60°.求山的高度BC.
如图,某登山队在山脚A处测得山顶B处的仰角为45°,沿坡角30°的斜坡AD前进1000m后到达D处,又测得山顶B处的仰角为60°.求山的高度BC.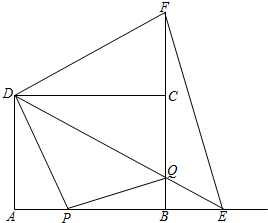 如图,矩形ABCD中,AB=8,AD=6.动点P从点A出发,沿线段AB(不包括端点A,B)以每秒2个单位长度的速度,匀速向点B运动;动点Q从点B出发,沿线段BC(不包括端点B,C)以每秒1个单位长度的速度,匀速向点C运动.连接DQ并延长交AB的延长线于点E,把DE沿DC翻折交BC延长线于点F,连接EF.点P,Q同时出发,同时停止,设运动时间为t秒.
如图,矩形ABCD中,AB=8,AD=6.动点P从点A出发,沿线段AB(不包括端点A,B)以每秒2个单位长度的速度,匀速向点B运动;动点Q从点B出发,沿线段BC(不包括端点B,C)以每秒1个单位长度的速度,匀速向点C运动.连接DQ并延长交AB的延长线于点E,把DE沿DC翻折交BC延长线于点F,连接EF.点P,Q同时出发,同时停止,设运动时间为t秒.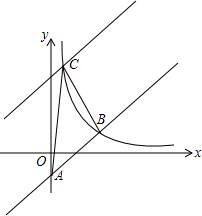 如图,在平面直角坐标系中直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
如图,在平面直角坐标系中直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).