题目内容
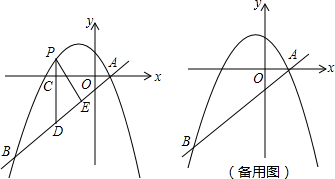
如图,在平面直角坐标系中,直线y=
x-
与抛物线y=-
x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.

考点:二次函数综合题
专题:压轴题
分析:(1)利用直线解析式求出点A、B的坐标,再利用待定系数法求二次函数解析式解答;
(2)①利用直线解析式和抛物线解析式表示出PD,再利用同角的余角相等求出∠DPE=∠BAO,根据直线k值求出∠BAO的正弦和余弦值,然后表示出PE、DE,再根据三角形的周长公式列式整理即可得解,再根据二次函数的最值问题解答;
②分(i)点G在y轴上时,过点P作PH⊥x轴于H,根据正方形的性质可得AP=AG,∠PAG=90°,再求出∠PAH=∠AGO,然后利用“角角边”证明△APH和△GAO全等,根据全等三角形对应边相等可得PH=AO=2,然后利用二次函数解析式求解即可;(ii)点F在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,根据正方形的性质可得AP=FP,∠APF=90°,再根据同角的余角相等求出∠APM=∠FPN,然后利用“角边角”证明△APM和△FPN全等,根据全等三角形对应边相等可得PM=PN,从而得到点P的横坐标与纵坐标相等,再根据二次函数的解析式求解即可.
(2)①利用直线解析式和抛物线解析式表示出PD,再利用同角的余角相等求出∠DPE=∠BAO,根据直线k值求出∠BAO的正弦和余弦值,然后表示出PE、DE,再根据三角形的周长公式列式整理即可得解,再根据二次函数的最值问题解答;
②分(i)点G在y轴上时,过点P作PH⊥x轴于H,根据正方形的性质可得AP=AG,∠PAG=90°,再求出∠PAH=∠AGO,然后利用“角角边”证明△APH和△GAO全等,根据全等三角形对应边相等可得PH=AO=2,然后利用二次函数解析式求解即可;(ii)点F在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,根据正方形的性质可得AP=FP,∠APF=90°,再根据同角的余角相等求出∠APM=∠FPN,然后利用“角边角”证明△APM和△FPN全等,根据全等三角形对应边相等可得PM=PN,从而得到点P的横坐标与纵坐标相等,再根据二次函数的解析式求解即可.
解答:解:(1)令y=0,则
x-
=0,解得x=2,
x=-8时,y=
×(-8)-
=-
,
∴点A(2,0),B(-8,-
),
把点A、B代入抛物线得,
,
解得
,
所以,该抛物线的解析式y=-
x2-
x+
;
(2)①∵点P在抛物线上,点D在直线上,
∴PD=-
x2-
x+
-(
x-
)=-
x2-
x+4,
∵PE⊥AB,
∴∠DPE+∠PDE=90°,
又∵PD⊥x轴,
∴∠BAO+∠PDE=90°,
∴∠DPE=∠BAO,
∵直线解析式k=
,
∴sin∠BAO=
,cos∠BAO=
,
∴PE=PDcos∠DPE=
PD,
DE=PDsin∠DPE=
PD,
∴△PDE的周长为l=PD+
PD+
PD=
PD=
(-
x2-
x+4)=-
x2-
x+
,
即l=-
x2-
x+
;
∵l=-
(x2+6x+9)+15,
∴当x=-3时,最大值为15;
②∵点A(2,0),
∴AO=2,
分(i)点G在y轴上时,过点P作PH⊥x轴于H,
在正方形APFG中,AP=AG,∠PAG=90°,
∵∠PAH+∠OAG=90°,∠AGO+∠OAG=90°,
∴∠PAH=∠AGO,
在△APH和△GAO中,
,
∴△APH≌△GAO(AAS),
∴PH=AO=2,
∴点P的纵坐标为2,
∴-
x2-
x+
=2,
整理得,x2+3x-2=0,
解得x=
,
∴点P1(
,2),P2(
,2);
(ii)点F在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,
在正方形APFG中,AP=FP,∠APF=90°,
∵∠APM+∠MPF=90°,∠FPN+∠MPF=90°,
∴∠APM=∠FPN,
在△APM和△FPN中,
,
∴△APM≌△FPN(AAS),
∴PM=PN,
∴点P的横坐标与纵坐标相等,
∴-
x2-
x+
=x,
整理得,x2+7x-10=0,
解得x1=
,x2=
(舍去),
∴点P3(
,
)
综上所述,存在点P1(
,2),P2(
,2),P3(
,
).
| 3 |
| 4 |
| 3 |
| 2 |
x=-8时,y=
| 3 |
| 4 |
| 3 |
| 2 |
| 15 |
| 2 |
∴点A(2,0),B(-8,-
| 15 |
| 2 |
把点A、B代入抛物线得,
|
解得
|
所以,该抛物线的解析式y=-
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
(2)①∵点P在抛物线上,点D在直线上,
∴PD=-
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
∵PE⊥AB,
∴∠DPE+∠PDE=90°,
又∵PD⊥x轴,
∴∠BAO+∠PDE=90°,
∴∠DPE=∠BAO,
∵直线解析式k=
| 3 |
| 4 |
∴sin∠BAO=
| 3 |
| 5 |
| 4 |
| 5 |
∴PE=PDcos∠DPE=
| 3 |
| 5 |
DE=PDsin∠DPE=
| 4 |
| 5 |
∴△PDE的周长为l=PD+
| 3 |
| 5 |
| 4 |
| 5 |
| 12 |
| 5 |
| 12 |
| 5 |
| 1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 5 |
| 18 |
| 5 |
| 48 |
| 5 |
即l=-
| 3 |
| 5 |
| 18 |
| 5 |
| 48 |
| 5 |
∵l=-
| 3 |
| 5 |
∴当x=-3时,最大值为15;
②∵点A(2,0),
∴AO=2,
分(i)点G在y轴上时,过点P作PH⊥x轴于H,
在正方形APFG中,AP=AG,∠PAG=90°,
∵∠PAH+∠OAG=90°,∠AGO+∠OAG=90°,
∴∠PAH=∠AGO,

在△APH和△GAO中,
|
∴△APH≌△GAO(AAS),
∴PH=AO=2,
∴点P的纵坐标为2,
∴-
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
整理得,x2+3x-2=0,
解得x=
-3±
| ||
| 2 |
∴点P1(
-3+
| ||
| 2 |
-3-
| ||
| 2 |
(ii)点F在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,
在正方形APFG中,AP=FP,∠APF=90°,
∵∠APM+∠MPF=90°,∠FPN+∠MPF=90°,
∴∠APM=∠FPN,
在△APM和△FPN中,
|
∴△APM≌△FPN(AAS),
∴PM=PN,
∴点P的横坐标与纵坐标相等,
∴-
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
整理得,x2+7x-10=0,
解得x1=
-7+
| ||
| 2 |
-7-
| ||
| 2 |
∴点P3(
-7+
| ||
| 2 |
-7+
| ||
| 2 |
综上所述,存在点P1(
-3+
| ||
| 2 |
-3-
| ||
| 2 |
-7+
| ||
| 2 |
-7+
| ||
| 2 |
点评:此题主要考查了二次函数的综合应用,全等三角形的判定与性质以及待定系数法求二次函数解析式,锐角三角函数的应用,(1)①利用锐角三角函数用PD表示出三角形是周长是解题的关键,②难点在于分情况讨论.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 如图,是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点,第三行有4个点,第四行有8个点,….那么这个三角点阵中前n行的点数之和可能是( )
如图,是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点,第三行有4个点,第四行有8个点,….那么这个三角点阵中前n行的点数之和可能是( )| A、510 | B、511 |
| C、512 | D、513 |
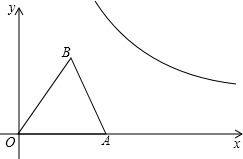 如图,已知等腰△AOB放置在平面直角坐标系xOy中,OA=OB,点B的坐标为(3,4).
如图,已知等腰△AOB放置在平面直角坐标系xOy中,OA=OB,点B的坐标为(3,4). 已知:如图,五边形ABCDE是正五边形,连接BD、CE,交于点P. 求证:四边形ABPE是平行四边形.
已知:如图,五边形ABCDE是正五边形,连接BD、CE,交于点P. 求证:四边形ABPE是平行四边形.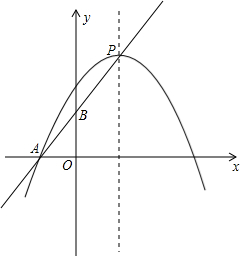 已知直线y=kx+3-k,当k=1,k=
已知直线y=kx+3-k,当k=1,k= 如图,在平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°,AB=2.求CF的长.
如图,在平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°,AB=2.求CF的长.