Question

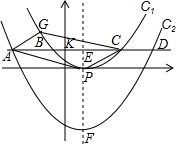已知顶点为P的抛物线C₁的解析式是y=a（x-3）²（a≠0），且经过点（0，1）．
（1）求a的值；
（2）如图将抛物线C₁向下平移h（h＞0）个单位得到抛物线C₂，过点K（0，m²）（m＞0）作直线l平行于x轴，与两抛物线从左到右分别相交于A、B、C、D四点，且A、C两点关于y轴对称．
①点G在抛物线C₁上，当m为何值时，四边形APCG是平行四边形？
②若抛物线C₁的对称轴与直线l交于点E，与抛物线C₂交于点F，试探究：在K点运动过程中，

KC

PF

的值是否会改变？若会，请说明理由；若不会，请求出这个值．

Answer 1

考点：二次函数综合题

专题：

分析：（1）直接利用待定系数法求二次函数解析式得出即可；
（2）首先得出△GQK≌△POK（ASA），进而得出顶点G在抛物线C₁上，得出2m²=

1

9

（-3-3）²，进而得出答案；
（3）利用函数对称性表示出A点坐标，再表示出KC，PF的长，进而得出其比值．

解答：解：（1）∵抛物线C₁的解析式是y=a（x-3）²（a≠0），经过点（0，1），
∴1=a（0-3）²，
解得：a=

1

9

，

（2）①∵A、C两点关于y轴对称，
∴点K为AC的中点，
若四边形APCG是平行四边形，则必有点K是PG的中点，
过点G作GQ⊥y轴于点Q，
在△GQK和△POK中

∠GQK=∠POK QK=OK ∠QKG=∠OKP

，
∴△GQK≌△POK（ASA），
∴GQ=PO=3，KQ=OK=m²，OQ=2m²，
∴点G（-3，2m²），
∵顶点G在抛物线C₁上，
∴2m²=

1

9

（-3-3）²，
解得：m=±

2

，
又∵m＞0，
∴m=

2

，
∴当m=

2

时，四边形APCG是平行四边形；

②

KC

PF

的值不会改变；
理由：在抛物线y=

1

9

（x-3）²中，令y=m²，
解得：x=3±3m，
又∵m＞0，且点C在点B的右侧，
∴C（3+3m，m²），KC=3+3m，
∵A、C两点关于y轴对称，
∴A（-3-3m，m²），
∵将抛物线C₁向下平移h（h＞0）个单位得到抛物线C₂，
∴抛物线C₂的解析式为：y=

1

9

（x-3）²-h，
∴m²=

1

9

（-3-3m-3）²-h，
解得：h=4m+4，
∴PF=4+4m，
∴

KC

PF

=

3+3m

4+4m

=

3

4

．

点评：此题主要考查了二次函数综合以及二次函数的平移以及全等三角形的判定与性质以及平行四边形的判定与性质等知识，利用二次函数对称性得出A点坐标是解题关键．