��Ŀ����
10�� ���壺���߳���������������������γ�Ϊ�����������Ρ���
���壺���߳���������������������γ�Ϊ�����������Ρ�����ѧѧϰС���ͬѧ��32���ȳ��Ļ�����ÿ�����ȼ�Ϊ1����λ����ȡ�� ���ɸ�����β���������������Σ�����̽�����
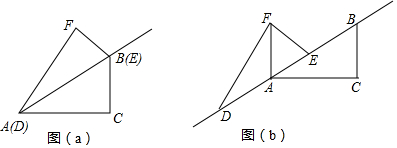
С����12���������ڳ���ͼ��ʾ�ġ����������Ρ���
Сӱ�ֱ���24����30�������ڳ�ֱ�ǡ����������Ρ���
С���ܵ�С����Сӱ���������ֱ�ڳ�������ͬ�ĵ��������������Ρ���
��1�����㻭��Сӱ��С�ڳ��ġ����������Ρ���ʾ��ͼ��
��2�����ܷ�Ҳ����ȡ�����ɸ��ڳ��ȱߡ����������Ρ�������ܣ��뻭��ʾ��ͼ��������ܣ���˵�����ɣ�
���� ��1������Ϊ�����������Ρ��Ķ��廭��ͼ�μ��ɣ�
��2�������ڣ���ȱ������εı߳�Ϊa����ȱ����������Ϊ$\frac{\sqrt{3}}{4}$a2����Ϊ�����߳�aΪ��������ô���$\frac{\sqrt{3}}{4}$a2һ�����������ɴ˼����жϣ�
��� �⣺��1��Сӱ�ڳ���ͼ1��ʾ�ġ����������Ρ���
С�ڳ���ͼ2��ʾ������ͬ�ĵ��������������Ρ���
��2�����ܰڳ��ȱߡ����������Ρ���
�������£���ȱ������εı߳�Ϊa����ȱ����������Ϊ$\frac{\sqrt{3}}{4}$a2��
��Ϊ�����߳�aΪ��������ô���$\frac{\sqrt{3}}{4}$a2һ����������
���Բ����ڵȱߡ����������Ρ���
���� ���⿼����ͼ-Ӧ�������ͼ�������������Ρ��Ķ��壬����Ĺؼ����������ѧ֪ʶ������⣬�����п�������Ŀ��

��ϰ��ϵ�д�
 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�����Ŀ
1�����¸����߶�Ϊ�߳������ֱ�������ε��ǣ�������
| A�� | 4��5��6 | B�� | 2��$\sqrt{2}$��4 | C�� | 11��12��13 | D�� | 5��12��13 |
18��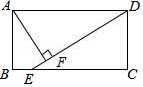 ��ͼ���ھ���ABCD�У�AD��AB������E��BC��һ�㣬��DE=DA��AF��DE������Ϊ��F�������н����У���һ����ȷ���ǣ�������
��ͼ���ھ���ABCD�У�AD��AB������E��BC��һ�㣬��DE=DA��AF��DE������Ϊ��F�������н����У���һ����ȷ���ǣ�������
 ��ͼ���ھ���ABCD�У�AD��AB������E��BC��һ�㣬��DE=DA��AF��DE������Ϊ��F�������н����У���һ����ȷ���ǣ�������
��ͼ���ھ���ABCD�У�AD��AB������E��BC��һ�㣬��DE=DA��AF��DE������Ϊ��F�������н����У���һ����ȷ���ǣ�������| A�� | AF=$\frac{1}{2}$AD | B�� | AB=AF | C�� | ��AFD�ա�DCE | D�� | BE=AD-DF |
5�����к����в���һ�κ������ǣ�������
| A�� | y=x | B�� | y=2x-1 | C�� | y=|x| | D�� | y=1-2x |
15���۲�����4�����⣺�����������ǣ�������
��1�������ε���Ǻ���180�㣻
��2�������ε������ڽ���������������ǣ�
��3��ֱ������������ǻ��ࣻ
��4����ȵĽ��ǶԶ��ǣ�
��1�������ε���Ǻ���180�㣻
��2�������ε������ڽ���������������ǣ�
��3��ֱ������������ǻ��ࣻ
��4����ȵĽ��ǶԶ��ǣ�
| A�� | ��1����2�� | B�� | ��2����3�� | C�� | ��2����4�� | D�� | ��3����4�� |
19�� ��ͼ����F��E�ֱ����߶�AB��CD�ϣ������������ж�AB��CD���ǣ�������
��ͼ����F��E�ֱ����߶�AB��CD�ϣ������������ж�AB��CD���ǣ�������
 ��ͼ����F��E�ֱ����߶�AB��CD�ϣ������������ж�AB��CD���ǣ�������
��ͼ����F��E�ֱ����߶�AB��CD�ϣ������������ж�AB��CD���ǣ�������| A�� | ��1=��2 | B�� | ��1=��4 | C�� | ��4=��2 | D�� | ��3=��4 |