Question

12．如图：已知△ABC中，AD是中线，且∠1=∠2，求证：AB=AC．

Answer 1

分析 过点D作DG⊥AB于点G，作DH⊥AC于点H，由角平分线的性质可得DG=DH，利用等积法可证得结论．

解答 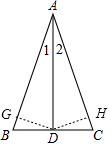证明：
∵AD为中线，
∴S_△ABD=S_△ADC，
如图，过点D作DG⊥AB于点G，作DH⊥AC于点H
则$\frac{1}{2}$DG•AB=$\frac{1}{2}$DH•AC，
∵∠1=∠2，
∴DG=DH，
∴AB=AC．

点评 本题主要考查角平分线的性质、中线的性质，构造三角形的高，利用等积法是解题的关键．