题目内容
12.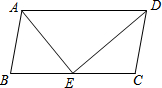 如图,在?ABCD中,DE是∠ADC的平分线,交BC于点E.
如图,在?ABCD中,DE是∠ADC的平分线,交BC于点E.(1)试说明CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
分析 (1)由平行四边形的性质可得AD∥BC,由平行线的性质得出和角平分线得出∠DEC=∠CDE,根据等角对等边可得CD=CE;
(2)证出BE=AB,由等腰三角形的性质和三角形内角和定理求出∠AEB,再由平行线的性质即可得出∠DAE=∠AEB=50°.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠ADE=∠DEC,
∵DE是∠ADC的平分线,
∴∠ADE=∠CDE,
∴∠DEC=∠CDE,
∴CD=CE;
(2)解:∵BE=CE,CD=CE,
∴BE=CD,
∵AB=CD,
∴BE=AB,
∴∠AEB=∠BAE=$\frac{1}{2}$(180°-∠B)=50°,
∵AD∥BC,
∴∠DAE=∠AEB=50°.
点评 此题主要考查了平行四边形的性质、等腰三角形的判定与性质、平行线的性质;熟练掌握平行四边形的性质,证明三角形是等腰三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下面各数中,既是分数,又是正数的是( )
| A. | 5 | B. | -2.25 | C. | 0 | D. | 8.3 |
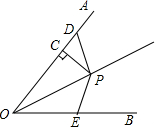 如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.
如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.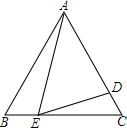 如图,等边三角形ABC的边长为5,点E为BC边上一点,且BE=2,点D为AC边上一点,若∠AED=60°,求CD的长?
如图,等边三角形ABC的边长为5,点E为BC边上一点,且BE=2,点D为AC边上一点,若∠AED=60°,求CD的长?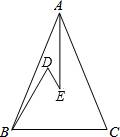 如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是8cm.
如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是8cm. 已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|+$\sqrt{m+n-18}$=0.
已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|+$\sqrt{m+n-18}$=0.