题目内容
18. 如图,CD是直角△ABC斜边上的中线,过点D作垂直于AB的直线交BC于点F,交AC的延长线于点E.
如图,CD是直角△ABC斜边上的中线,过点D作垂直于AB的直线交BC于点F,交AC的延长线于点E.(1)求证:△ADE∽△FDB;
(2)若DF=2,EF=6,求CD的长.
分析 (1)根据题意,得∠A+∠B=90°,∠A+∠E=90°,则∠E=∠B,易证△ADE∽△FDB;
(2)由Rt△ABC中,CD是斜边上的中线,得AD=CD=BD=$\frac{1}{2}$AB,由(1)中的结论,得出$\frac{AD}{FD}$=$\frac{DE}{DB}$,进一步整理代入求得答案即可.
解答 (1)证明:∵DE⊥AB,
∴∠ADE=∠FDB=90°,
∴∠A+∠E=90°,
∵Rt△ABC中∠A+∠B=90°,
∴∠E=∠B,
∴△ADE∽△FDB …(4分)
(2)解:∵CD是直角△ABC斜边上的中线,
∴AD=CD=BD=$\frac{1}{2}$AB,
∵△ADE∽△FDB,
∴$\frac{AD}{FD}$=$\frac{DE}{DB}$,
∵DF=2,EF=6,
∴DE=8
∴$\frac{\frac{1}{2}AB}{2}$=$\frac{8}{\frac{1}{2}AB}$,
∴AB=8,
∴CD=4.
点评 本题主要考查了直角三角形和相似三角形的判定与性质,掌握直角三角形斜边上的中线等于斜边的一半,是解答本题的关键.

练习册系列答案
相关题目
3.等腰三角形的一个底角是50°,则它的顶角是( )
| A. | 50° | B. | 50°或65° | C. | 65° | D. | 80° |
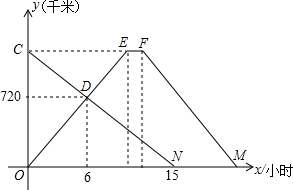 快车甲和慢车乙分别从A、B两站同时出发,相向而行.快车到达B站后,停留1小时,然后原路原速返回A站,慢车到达A站即停运休息.如图表示的是两车离A站的距离y(千米)与行驶时间x(小时)的函数图象.请结合图象信息,解答下列问题:
快车甲和慢车乙分别从A、B两站同时出发,相向而行.快车到达B站后,停留1小时,然后原路原速返回A站,慢车到达A站即停运休息.如图表示的是两车离A站的距离y(千米)与行驶时间x(小时)的函数图象.请结合图象信息,解答下列问题: