题目内容
6.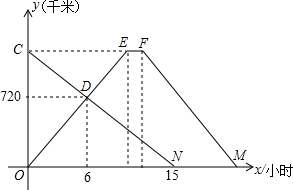 快车甲和慢车乙分别从A、B两站同时出发,相向而行.快车到达B站后,停留1小时,然后原路原速返回A站,慢车到达A站即停运休息.如图表示的是两车离A站的距离y(千米)与行驶时间x(小时)的函数图象.请结合图象信息,解答下列问题:
快车甲和慢车乙分别从A、B两站同时出发,相向而行.快车到达B站后,停留1小时,然后原路原速返回A站,慢车到达A站即停运休息.如图表示的是两车离A站的距离y(千米)与行驶时间x(小时)的函数图象.请结合图象信息,解答下列问题:(1)直接写出快、慢两车的速度及A、B两站间的距离;
(2)求快车从B返回A站时,y与x之间的函数关系式;
(3)出发几小时,两车相距300千米?请直接写出答案.
分析 (1)根据图中数据得出两车行驶的距离与行驶时间的关系,进而得出两车的速度;
(2)根据两车的速度、距离和时间得出E、F、M点坐标,然后设直线MF解析式,根据待定系数法即可求得;
(3)根据两车相遇前和两车相遇后两车距离为300千米两种情况分别列方程,解方程即可.
解答 解:(1)由图象知快车经过6小时行驶了720千米,慢车经过(15-6)小时行驶了720千米,
所以,快车的速度:720÷6=120(千米/时),慢车的速度:720÷(15-6)=80(千米/时);
(2)A、B两站的距离:80×15=1200(千米),那么快车甲到B站的时间:1200÷120=10(小时),则E(10,1200),到达B站后,停留1小时,则F(11,1200),根据题意M(21,0),
设直线FM的解析式为y=kx+b,则
$\left\{\begin{array}{l}{1200=11k+b}\\{0=21k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-120}\\{b=2520}\end{array}\right.$,
故快车从B返回A站时,y与x之间的函数关系式为y=-120x+2520(11≤x≤21);
(3)设出发x小时,两车相距300千米,
根据题意得,
相遇前:120x+80x+300=1200,解得x=4.5;
相遇后:120x+80x-300=1200,解得x=7.5.
答:出发4.5小时和7.5小时时,两车相距300千米.
点评 此题主要考查了一次函数的应用,根据已知图象点的坐标得出其他点的坐标是解题关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
11.下列运算中结果正确的是( )
| A. | -3x+5x=-8x | B. | 5y-3y=2 | C. | 3x2y-2x2y=x2y | D. | 3a+2b=5ab |
15.求$\frac{49}{81}$的平方根的数学表达式为( )
| A. | $\sqrt{\frac{49}{81}}$=±$\frac{7}{9}$ | B. | $\sqrt{\frac{49}{81}}$=-$\frac{7}{9}$ | C. | ±$\sqrt{\frac{49}{81}}$=±$\frac{7}{9}$ | D. | $\sqrt{\frac{49}{81}}$=$\frac{7}{9}$ |
16.化简$\sqrt{-x{y}^{2}}$(y<0)的结果是( )
| A. | y$\sqrt{x}$ | B. | y$\sqrt{-x}$ | C. | -y$\sqrt{x}$ | D. | -y$\sqrt{-x}$ |
 如图,CD是直角△ABC斜边上的中线,过点D作垂直于AB的直线交BC于点F,交AC的延长线于点E.
如图,CD是直角△ABC斜边上的中线,过点D作垂直于AB的直线交BC于点F,交AC的延长线于点E.