题目内容
2.关于x、y的方程组$\left\{\begin{array}{l}{x+2y=4k}\\{2x+y=2k+1}\end{array}\right.$的解满足x-y=13.求k的值.分析 将k看做已知数表示出x与y,代入x-y=13即可求出k的值.
解答 解:$\left\{\begin{array}{l}{x+2y=4k①}\\{2x+y=2k+1②}\end{array}\right.$,
①×2-②得:$y=\frac{6k-1}{3}$,
②×2-①得:x=$\frac{2}{3}$,
把$y=\frac{6k-1}{3}$,x=$\frac{2}{3}$代入x-y=13得:$\frac{2}{3}$-$\frac{6k-1}{3}$=13,
解得:k=-6.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.工人师傅在架设电线时,为了检验三条电线是否平行,工人师傅只检验其中两条是否与第三条平行即可,这种做法的依据是( )
| A. | 两点确定一条直线 | |
| B. | 两点之间,线段最短 | |
| C. | 经过直线外一点有且只有一条直线与已知直线平行 | |
| D. | 如果两条直线都和第三条直线平行,那么这两条直线也相互平行 |
11.若式子$\sqrt{x-7}$在实数范围内有意义,则x的取值范围是( )
| A. | x<7 | B. | x≤7 | C. | x>7 | D. | x≥7 |
 如图,等腰梯形ABCD中,AB∥DC,AD=BC=8,AB=10,CD=6,则梯形ABCD的面积等于16$\sqrt{15}$.
如图,等腰梯形ABCD中,AB∥DC,AD=BC=8,AB=10,CD=6,则梯形ABCD的面积等于16$\sqrt{15}$.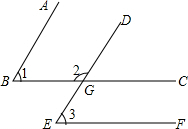 如图,已知∠1=∠3,∠2与∠3互补,AB∥DE吗?BC∥EF吗?为什么?
如图,已知∠1=∠3,∠2与∠3互补,AB∥DE吗?BC∥EF吗?为什么?