题目内容
13．
如图，等腰梯形ABCD中，AB∥DC，AD=BC=8，AB=10，CD=6，则梯形ABCD的面积等于16$\sqrt{15}$．
分析 知道等腰梯形的上底、下底，只要求出高，就可得梯形的面积．
解答 解：过D，C分别作高DE，CF，垂足分别为E，F
，
∵等腰梯形ABCD中，AB∥DC，AD=BC=8，AB=10，CD=6，
∴DC=EF=6，AE=BF=2，
∴DE=2$\sqrt{15}$，
∴梯形ABCD的面积=（6+10）×2$\sqrt{15}$÷2=16$\sqrt{15}$，
故答案为：16$\sqrt{15}$．
点评 此题主要考查学生对等腰梯形的性质及梯形的面积公式的掌握及运用能力，解题的关键是正确的构造直角三角形，难度不大．
练习册系列答案
相关题目
1．
如图所示，在△ABC中，AB=AC，AB的垂直平分线分别交AC、AB于D、E，若△ABC和△DBC的周长分别为40cm和25cm，则BC等于（ ）
如图所示，在△ABC中，AB=AC，AB的垂直平分线分别交AC、AB于D、E，若△ABC和△DBC的周长分别为40cm和25cm，则BC等于（ ）| A． | 5cm | B． | 10cm | C． | 15cm | D． | 12cm |
8．
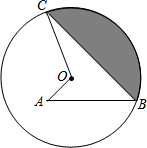如图，已知点A为⊙O内一点，点B、C均在圆上，∠C=30°，∠A=∠B=45°，线段OA=$\sqrt{3}$-1，则阴影部分的周长为（ ）
如图，已知点A为⊙O内一点，点B、C均在圆上，∠C=30°，∠A=∠B=45°，线段OA=$\sqrt{3}$-1，则阴影部分的周长为（ ）| A． | $\frac{4π}{3}$+2$\sqrt{3}$ | B． | $\frac{2π}{3}$+2$\sqrt{3}$ | C． | $\frac{4π}{3}$+$\sqrt{3}$ | D． | $\frac{2π}{3}$+$\sqrt{3}$ |
如图，抛物线y=ax2+bx+4与x轴的两个交点分别为A（-4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．
已知Rt△ABC中，∠C=90°，D为AB上的中点．CE⊥AB于E，CD=5，BC=6．求AC，CE的长．
3．
如图为某几何体的示意图，则该几何体的俯视图为（ ）
如图为某几何体的示意图，则该几何体的俯视图为（ ）| A． |  | B． |  | C． |  | D． |  |