题目内容
17．
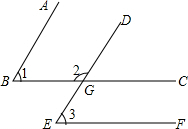如图，已知∠1=∠3，∠2与∠3互补，AB∥DE吗？BC∥EF吗？为什么？
分析 由条件可求得∠1和∠2互补，可证明AB∥DE，利用对顶角相等可得∠CGE和∠3互补，可证明BC∥EF．
解答 解：
∵∠2和∠3互补，
∴∠2+∠3=180°，
∵∠1=∠3，
∴∠1+∠2=180°，
∴AB∥DE；
∵∠2=∠CGE，
∴∠3+∠CGE=180°，
∴BC∥EF．
点评 本题主要考查平行线的判定，掌握平行线的性质和判定是解题的关键，即①同位角相等?两直线平行，②内错角相等?两直线平行，③同旁内角互补?两直线平行，④a∥b，b∥c⇒a∥c．
练习册系列答案
相关题目
7．用反证法证明命题：在一个三角形中，至少有一个内角不大于60°．证明的第一步是（ ）
| A． | 假设三个内角都不大于60° | B． | 假设三个内角都大于60° | ||
| C． | 假设三个内角至多有一个大于60° | D． | 假设三个内角至多有两个大于60° |
8．
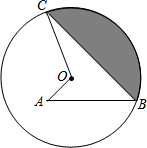如图，已知点A为⊙O内一点，点B、C均在圆上，∠C=30°，∠A=∠B=45°，线段OA=$\sqrt{3}$-1，则阴影部分的周长为（ ）
如图，已知点A为⊙O内一点，点B、C均在圆上，∠C=30°，∠A=∠B=45°，线段OA=$\sqrt{3}$-1，则阴影部分的周长为（ ）| A． | $\frac{4π}{3}$+2$\sqrt{3}$ | B． | $\frac{2π}{3}$+2$\sqrt{3}$ | C． | $\frac{4π}{3}$+$\sqrt{3}$ | D． | $\frac{2π}{3}$+$\sqrt{3}$ |
已知Rt△ABC中，∠C=90°，D为AB上的中点．CE⊥AB于E，CD=5，BC=6．求AC，CE的长．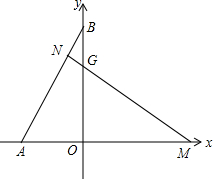
在平面直角坐标中，x轴上有点A和点M，y轴上有一点B，过点M作MN⊥AB于点N，交y轴于点G，且MG=AB，OA、OM（OA＜OM）的长是方程x2-7x+12=0的两个根．
“魔术塑料积木”可以开发智力、发挥想像空间．如图是小明用六个棱长为1的立方块组成的一个几何体，其俯视图的面积是5．
7．如图是我国几家银行的标志，在这几个图形中是轴对称图形的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |