题目内容
12．（1）计算：（3x-5）2-（2x+7）2；（2）分解因式：ax2+2a2x+a3．
分析 （1）直接利用平方差公式分解因式进而化简求出即可；
（2）首先提取公因式a，再利用完全平方公式分解因式得出即可．
解答 解：（1）（3x-5）2-（2x+7）2
=（3x-5+2x+7）（3x-5-2x-7）
=（5x+2）（x-12）；
（2）ax2+2a2x+a3
=a（x2-2ax+a2）
=a（x-a）2．
点评 此题主要考查了完全平方公式以及平方差公式分解因式，熟练应用乘法公式是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
作图题：
20．若关于x的方程$\frac{x}{x-1}$-2=$\frac{m}{x-1}$无解，则m的值是（ ）
| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
7．用反证法证明命题：在一个三角形中，至少有一个内角不大于60°．证明的第一步是（ ）
| A． | 假设三个内角都不大于60° | B． | 假设三个内角都大于60° | ||
| C． | 假设三个内角至多有一个大于60° | D． | 假设三个内角至多有两个大于60° |
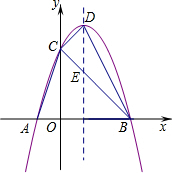如图，抛物线y=-x2+bx+c与x轴交于A（-1，0）、B（3，0）两点，与y轴相交于点C，顶点为D．
1．
如图所示，在△ABC中，AB=AC，AB的垂直平分线分别交AC、AB于D、E，若△ABC和△DBC的周长分别为40cm和25cm，则BC等于（ ）
如图所示，在△ABC中，AB=AC，AB的垂直平分线分别交AC、AB于D、E，若△ABC和△DBC的周长分别为40cm和25cm，则BC等于（ ）| A． | 5cm | B． | 10cm | C． | 15cm | D． | 12cm |