题目内容
3. 如图,点P是一次函数与反比例函数图象交于第一象限内的点,PA⊥x轴于点A,PB⊥y轴于点B,一次函数图象分别交x轴、y轴于点C、D,且S△PAC=1,$\frac{OB}{OD}$=$\frac{1}{2}$,tan∠ACP=$\frac{1}{2}$.求:
如图,点P是一次函数与反比例函数图象交于第一象限内的点,PA⊥x轴于点A,PB⊥y轴于点B,一次函数图象分别交x轴、y轴于点C、D,且S△PAC=1,$\frac{OB}{OD}$=$\frac{1}{2}$,tan∠ACP=$\frac{1}{2}$.求:(1)点D的坐标(0,-2);
(2)一次函数与反比例函数的解析式;
(3)根据图象直接写出:当x>0,一次函数的值小于反比例函数的值时,自变量x的取值范围.
分析 (1)由一次函数y=kx+b可知,D点坐标为(0,b),即OD=-b,结合tan∠ACP=$\frac{1}{2}$,S△PAC=1,求出b的值,D点的坐标即可求出;
(2)在Rt△ODC,tan∠OCD=tan∠ACP=$\frac{1}{2}$,再求出P点坐标,于是可以求出一次函数与反比例函数的解析式;
(3)由两函数的图象直接写出x的取值范围即可.
解答 解:(1)由一次函数y=kx+b可知,D点坐标为(0,b),即OD=-b.
∵$\frac{OB}{OD}$=$\frac{1}{2}$,
∴OB=-$\frac{1}{2}$b.
∵PA⊥x轴于点A,PB⊥y轴于点B,
∴四边形OAPB为矩形.
∴PA=0B=-$\frac{1}{2}$b.
在Rt△PAC中,tan∠ACP=$\frac{1}{2}$,
∴AC=-b,
∵S△PAC=1,
∴b=-2,即D点坐标为(0,-2);
故答案为(0,-2);
(2)在Rt△ODC,tan∠OCD=tan∠ACP=$\frac{1}{2}$,
∴OC=2OD=4,OA=6,
∴P点的坐标为(6,1),
∴一次函数与反比例函数的解析式分别为y=$\frac{1}{2}$x-2、y=$\frac{6}{x}$;
(3)由图象可知,一次函数与反比例函数图象的交点为P(6,1),
当0<x<6时一次函数的值小于反比例函数的值.
点评 本题是一道反比例函数的综合试题,考查了待定系数法求反比例函数的解析式和求一次函数的解析式,由图象特征确定自变量的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.将0.000000135用科学记数法可表示为( )
| A. | 0.135×10-7 | B. | 1.35×10-6 | C. | 1.35×10-8 | D. | 1.35×10-7 |
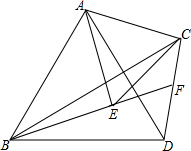 如图,在△ABC中,分别以AB、AC为边作等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,求证:
如图,在△ABC中,分别以AB、AC为边作等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,求证: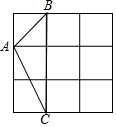 在方格中,若三角形的顶点都落在格点上,则这个三角形叫格点三角形,在3×3的方格中,与图中△ABC相似的格点三角形(不含△ABC)有( )
在方格中,若三角形的顶点都落在格点上,则这个三角形叫格点三角形,在3×3的方格中,与图中△ABC相似的格点三角形(不含△ABC)有( ) 如图,在△ABC中,点D,E分别是边AB,BC的中点,若DE的长是6,则AC的长等于12.
如图,在△ABC中,点D,E分别是边AB,BC的中点,若DE的长是6,则AC的长等于12. 如图,平行四边形ABCD的对角线相交于O点,则图中有4对全等三角形.
如图,平行四边形ABCD的对角线相交于O点,则图中有4对全等三角形.