题目内容
13. 如图,平行四边形ABCD的对角线相交于O点,则图中有4对全等三角形.
如图,平行四边形ABCD的对角线相交于O点,则图中有4对全等三角形.
分析 根据平行四边形的性质及全等三角形的判定方法进行分析,从而得到答案.
解答 解:∵ABCD是平行四边形
∴AD=BC,AB=CD,AO=CO,BO=DO,
在△ABO和△CDO中,$\left\{\begin{array}{l}{OA=OC}&{\;}\\{∠AOB=∠COD}&{\;}\\{OB=OD}&{\;}\end{array}\right.$,
∴△ABO≌△CDO(SAS),
同理:△ADO≌△CBO;
在△ABD和△CDB中,$\left\{\begin{array}{l}{AB=CD}&{\;}\\{AD=CB}&{\;}\\{BD=DB}&{\;}\end{array}\right.$,
∴△ABD≌△CDB(SSS),
同理:△ACD≌△CAB;
∴图中的全等三角形共有4对.
故答案为:4.
点评 本题主要考查了平行四边形的性质、全等三角形的判定;熟记平行四边形的性质是解决问题的关键.

练习册系列答案
相关题目
4.一个边长是31.4厘米的正方形纸片,围成一个圆柱体的侧面(接头处不重叠),这个圆柱体的底面半径是( )
| A. | 5厘米 | B. | 10厘米 | C. | 15厘米 | D. | 20厘米 |
8. 如图,在△ABC中∠B=30°,∠C=90°,AD是∠CAB的平分线,DE⊥AC于点E,DE=1,则BC的长是( )
如图,在△ABC中∠B=30°,∠C=90°,AD是∠CAB的平分线,DE⊥AC于点E,DE=1,则BC的长是( )
 如图,在△ABC中∠B=30°,∠C=90°,AD是∠CAB的平分线,DE⊥AC于点E,DE=1,则BC的长是( )
如图,在△ABC中∠B=30°,∠C=90°,AD是∠CAB的平分线,DE⊥AC于点E,DE=1,则BC的长是( )| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | $\sqrt{3}+2$ |
2.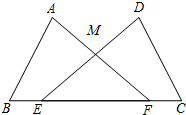 如图,点E,F在线段BC上,△ABF与△DEC全等,其中点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DEC等于( )
如图,点E,F在线段BC上,△ABF与△DEC全等,其中点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DEC等于( )
 如图,点E,F在线段BC上,△ABF与△DEC全等,其中点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DEC等于( )
如图,点E,F在线段BC上,△ABF与△DEC全等,其中点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DEC等于( )| A. | ∠B | B. | ∠A | C. | ∠EMF | D. | ∠AFB |
3.在反比例函数y=$\frac{2-k}{x}$的图象上有两点A(x1,y1)、B(x2,y2).若x1<0<x2,y1>y2,则k取值范围是
( )
( )
| A. | k≥2 | B. | k>2 | C. | k≤2 | D. | k<2 |
 如图,点P是一次函数与反比例函数图象交于第一象限内的点,PA⊥x轴于点A,PB⊥y轴于点B,一次函数图象分别交x轴、y轴于点C、D,且S△PAC=1,$\frac{OB}{OD}$=$\frac{1}{2}$,tan∠ACP=$\frac{1}{2}$.求:
如图,点P是一次函数与反比例函数图象交于第一象限内的点,PA⊥x轴于点A,PB⊥y轴于点B,一次函数图象分别交x轴、y轴于点C、D,且S△PAC=1,$\frac{OB}{OD}$=$\frac{1}{2}$,tan∠ACP=$\frac{1}{2}$.求: