题目内容
14. 如图,已知△ABC内接于⊙O,CD是⊙O的切线与半径OB的延长线交于点D,∠A=30°,求∠BCD的度数.
如图,已知△ABC内接于⊙O,CD是⊙O的切线与半径OB的延长线交于点D,∠A=30°,求∠BCD的度数.
分析 如图,连接OC. 构建直角△OCD和等边△OBC,结合图形,可以得到∠BCD=90°-∠OCB=30°.
解答  解:如图,连接OC.
解:如图,连接OC.
∵CD是⊙O的切线,
∴∠OCD=90°.
∵∠A=30°,
∴∴∠COB=2∠=60°.
∵OC=OB,
∴△OBC是等边三角形,
∴∠OCB=60°,
∴∠BCD=90°-∠OCB=30°.
点评 本题考查了切线的性质和圆周角定理.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
2.三角形两边长为4和11,第三边长为3-6m,则m的取值范围是( )
| A. | -2<m<-$\frac{2}{3}$ | B. | m>-2 | C. | -2≤m≤-$\frac{2}{3}$ | D. | m<-2 |
19.某中学要组织一次篮球比赛,赛制为单循环形式(毎两队之间都赛一场),计划安排21场比赛,求参加的球队支数,如果设参加的球队支数为x,则可列方程为( )
| A. | $\frac{1}{2}$x(x+1)=21 | B. | x(x+1)=21 | C. | $\frac{1}{2}$x(x-1)=21 | D. | x(x-1)=21 |
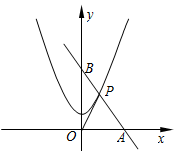 已知,如图,直线AB经过点B(0,6),且tan∠ABO=$\frac{2}{3}$,与抛物线y=ax2+2在第一象限内相交于点P,又知△AOP的面积为6.
已知,如图,直线AB经过点B(0,6),且tan∠ABO=$\frac{2}{3}$,与抛物线y=ax2+2在第一象限内相交于点P,又知△AOP的面积为6.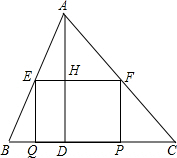 如图所示,在△ABC中,BC=10,高AD=8,矩形=EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图所示,在△ABC中,BC=10,高AD=8,矩形=EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H. 如图所示,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是②或③或④.
如图所示,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是②或③或④.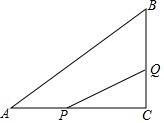 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动