题目内容
2．三角形两边长为4和11，第三边长为3-6m，则m的取值范围是（ ）| A． | -2＜m＜-$\frac{2}{3}$ | B． | m＞-2 | C． | -2≤m≤-$\frac{2}{3}$ | D． | m＜-2 |
分析 根据三角形的三边关系定理可得11-4＜3-6m＜4+11，再解即可．
解答 解：由题意得：11-4＜3-6m＜4+11，
解得：-2＜m＜-$\frac{2}{3}$，
故选：A．
点评 此题主要考查了三角形的三边关系，关键是掌握三角形两边之和大于第三边，三角形的两边差小于第三边．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
10．已知a-b=3，ab=2，则a2-ab+b2的值为（ ）
| A． | 9 | B． | 13 | C． | 11 | D． | 8 |
7．有一张长方形纸片ABCD，按下面步骤进行折叠：
第一步：如图①，点E在边BC上，沿AE折叠，点B落在点B′处；
第二步：如图②，沿EB′折叠，使点A落在BC延长线上的点A′处，折痕为EF．
有下列结论：①△AEF是等边三角形；②EF垂直平分AA′；③CA′=FD．（ ）
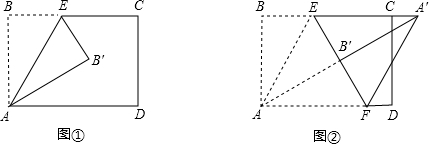
第一步：如图①，点E在边BC上，沿AE折叠，点B落在点B′处；
第二步：如图②，沿EB′折叠，使点A落在BC延长线上的点A′处，折痕为EF．
有下列结论：①△AEF是等边三角形；②EF垂直平分AA′；③CA′=FD．（ ）
| A． | 只有②正确 | B． | 只有①②正确 | C． | 只有①③正确 | D． | ①②③都正确 |
如图，已知△ABC内接于⊙O，CD是⊙O的切线与半径OB的延长线交于点D，∠A=30°，求∠BCD的度数．
12．下列去括号运算中，正确的是（ ）
| A． | a2-（a-2b+3c）=a2-a-2b+3c | B． | a+（-x+y-2）=a-x-y-2 | ||
| C． | （2a+b）-2（a2-b2）=2a+b-2a2+b2 | D． | -（x+y）+（a-1）=-x-y+a |