Question

如图，已知△ABC是等腰直角三角形，CD是斜边AB的中线，△ADC绕点D旋转一定角度得到△A'DC'，A'D交AC于点E，DC'交BC于点F，连接EF，若，则=　　．

　

Answer 1

【考点】旋转的性质；平行线的判定；全等三角形的判定与性质；等腰直角三角形；平行线分线段成比例．

【专题】压轴题．

【分析】根据等腰直角三角形的性质及旋转的性质，运用“ASA”证明△ADE≌△CDF，得DE=DF．则有DE：DA′=DF：DC′，得EF∥A′C′．根据相似三角形性质求解．

【解答】解：∵△ABC是等腰直角三角形，CD是斜边AB的中线，

∴CD⊥AB，CD=AD，∠A=∠BCD=45°．

又∵∠ADE=90°﹣∠CDE=∠CDF，

∴△ADE≌△CDF （ASA）

∴DE=DF．

∵DA=DA′，DC=DC′，

∴DE：DA′=DF：DC′，

∴EF∥A′C′．

∴△DEF∽△DA′C′，

∴．

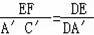
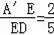
∵，则，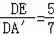

∴．

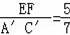
故答案为．

【点评】此题考查等腰三角形性质、旋转的性质、全等三角形的判定与性质及平行线的判定和性质等知识点，综合性较强．