题目内容
20．如果关于x的不等式组$\left\{\begin{array}{l}{x-a＞0，①}\\{x-a＜1，②}\end{array}\right.$的解集中，任意一个x值均不在3≤x≤6的范围内，求a的取值范围．分析 先解不等式组得到a＜x＜1+a，由于任意一个x值均不在3≤x≤6的范围内，所以1+a≤3或a≥6，然后解关于a的不等式即可．
解答 解：解①得x＞a，
解②得x＜1+a，
所以不等式的解集为a＜x＜1+a，
因为任意一个x值均不在3≤x≤6的范围内，
所以1+a≤3或a≥6，
即a的范围为a≤2或a≥6．
点评 本题考查了不等式的解集：能使不等式成立的未知数的取值范围，叫做不等式的解的集合，简称解集．
练习册系列答案
相关题目
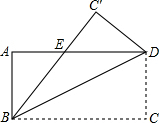如图，将长方形ABCD沿对角线BD折叠，使C恰好落在C'位置，∠DBC=25°，则∠ABC'=40°．
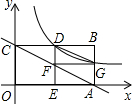如图，已知矩形OABC中，点A（2，0）、C（0，1）．点D是边BC的中点，过点D作DE⊥OA于点E，双曲线y=$\frac{k}{x}$过点D交AB于点G，直线AC交DE于点F，连接DG、FG．