题目内容
8.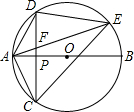 如图,AB是⊙O直径,弦CD⊥AB于P,E是⊙O上一点,连结AD、AC、AE、DE、CE.
如图,AB是⊙O直径,弦CD⊥AB于P,E是⊙O上一点,连结AD、AC、AE、DE、CE.求证:
(1)AE平分∠CED;
(2)AC2=AE•AF.
分析 (1)由垂径定理得出$\widehat{AD}=\widehat{AC}$,由圆周角定理得出∠AED=∠AEC,即可得出结论;
(2)由圆周角定理得出∠ACD=∠AEC,再由公共角∠CAF=∠EAC,政策△ACF∽△AEC,得出对应边成比例AC:AE=AF:AC,即可得出结论.
解答 证明:(1)∵AB是⊙O直径,弦CD⊥AB,
∴$\widehat{AD}=\widehat{AC}$,
∴∠AED=∠AEC,
∴AE平分∠CED;
(2)∵$\widehat{AD}=\widehat{AC}$,
∴∠ACD=∠AEC,
又∵∠CAF=∠EAC,
∴△ACF∽△AEC,
∴AC:AE=AF:AC,
∴AC2=AE•AF.
点评 本题考查了垂径定理、圆周角定理、相似三角形的判定与性质;熟练掌握垂径定理,证明三角形相似得出比例式是解决问题(2)的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
19.计算a6•a2的结果是( )
| A. | a4 | B. | a8 | C. | a12 | D. | a3 |
 将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEF=70°,则∠AED=55°.
将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEF=70°,则∠AED=55°. 如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)
如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示) 已知二次函数y=2x2-4x-6.
已知二次函数y=2x2-4x-6. 已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.