题目内容
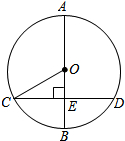 如图,AB是⊙O的直径,弦CD⊥AB于点E,连结OC,若OE=
如图,AB是⊙O的直径,弦CD⊥AB于点E,连结OC,若OE=| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:垂径定理,解直角三角形
专题:
分析:设OC=5x,OE=3x,在Rt△OEC中,由勾股定理求出CE=4x,解直角三角形求出即可.
解答:解:∵OA=OC,OE=
OA,
∴OE=
OC,
设OC=5x,OE=3x,
在Rt△OEC中,由勾股定理得:CE=4x,
则tan∠COE=
=
=
,
故选D.
| 3 |
| 5 |
∴OE=
| 3 |
| 5 |
设OC=5x,OE=3x,
在Rt△OEC中,由勾股定理得:CE=4x,
则tan∠COE=
| CE |
| OE |
| 4x |
| 3x |
| 4 |
| 3 |
故选D.
点评:本题考查了解直角三角形,勾股定理的应用,解此题的关键是求出OE=3x,CE-4x,题目比较好,难度适中.

练习册系列答案
相关题目
下列命题中,正确的命题是( )
| A、圆的切线垂直于圆的半径 |
| B、经过三个点一定可以作圆 |
| C、三角形的外心到三角形各顶点的距离都相等 |
| D、平分弦的直径必垂直于弦 |
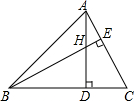 如图,在△ABC中,∠ABC=45°,AC=8,H是高AD和BE的交点,则线段BH的长度为
如图,在△ABC中,∠ABC=45°,AC=8,H是高AD和BE的交点,则线段BH的长度为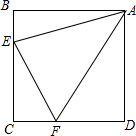 如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小.
如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小. 如图,在梯形ABCD中,已知AE平分∠BAD,AB=AD+BC,E是CD的中点.求证:BE平分∠ABC.
如图,在梯形ABCD中,已知AE平分∠BAD,AB=AD+BC,E是CD的中点.求证:BE平分∠ABC. 如图,在四边形ABCD中,AB=DC,∠ABC=∠DCB,点E、F分别在AB、BC上,且BE=2AE,CF=2DF.求证:∠BEC=∠CFB.
如图,在四边形ABCD中,AB=DC,∠ABC=∠DCB,点E、F分别在AB、BC上,且BE=2AE,CF=2DF.求证:∠BEC=∠CFB. 如图,在△ABC内的点P分别作三边的平行线.形成三个小三角形①②③,已知这三个三角形的面积分别是4,9,16,求△ABC的面积.
如图,在△ABC内的点P分别作三边的平行线.形成三个小三角形①②③,已知这三个三角形的面积分别是4,9,16,求△ABC的面积. 如图,⊙O的半径为2.5,动点P到定点O的距离为2,动点Q到P点的距离为1,则点P、Q与⊙O有何位置关系?说明理由.
如图,⊙O的半径为2.5,动点P到定点O的距离为2,动点Q到P点的距离为1,则点P、Q与⊙O有何位置关系?说明理由.