Question

如图，D是Rt△ABC的直角边BC上的点，以BD为直径的⊙O交斜边AB于E，EC交⊙O于点F，BF的延长线交AC于点G，求证：FG•AC=FC•AE．

Answer 1

考点：相似三角形的判定与性质,圆周角定理

专题：证明题

分析：利用条件可得出∠CGF=∠CEA，可证明△CGF∽△CEA，利用相似三角形的性质可得出结论．

解答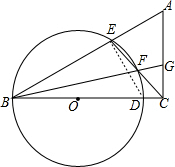：证明：连接DE，
∵BD为直径，
∴∠DEA=90°，
∴∠AEC=90°-∠DEC，且∠DEC=∠GBC，
∴∠AEC=90°-∠GBC，
∵∠ACB=90°，
∴∠BGC=90°-∠GBC，
∴∠CGF=CEA，且∠GCF=∠ECA，
∴△CGF∽△CEA，
∴

FC

AC

=

FG

AE

，
∴FG•AC=FC•AE．

点评：本题主要考查相似三角形的判定和性质，掌握同弧所对的圆周角相等是解题的关键．化线段乘积为线段比例是解决这类问题的常用思路．