题目内容
20.先化简,再求值:$\frac{{a}^{2}-3a}{{a}^{2}+a}$÷$\frac{a-3}{{a}^{2}-1}$-$\frac{3a+3}{a+1}$(其中a=$\frac{1}{{\sqrt{2}-1}}$)分析 先算除法,再算减法,最后把a的值代入进行计算即可.
解答 解:原式=$\frac{a-3}{a+1}$•$\frac{(a+1)(a-1)}{a-3}$-$\frac{3(a+1)}{a+1}$
=(a-1)-3
=a-1-3
=a-4.
当a=$\frac{1}{\sqrt{2}-1}$时,原式=$\frac{1}{\sqrt{2}-1}$-4=$\sqrt{2}$-3.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
10.已知直线y=kx+b,其中k+b=-5,kb=6,那么直线经过象限为( )
| A. | 第二、四 | B. | 第二、三、四 | C. | 第一、三 | D. | 第一、二、三 |
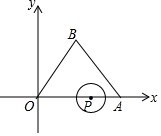 如图,等边三角形OAB的边长为8,点P沿O→A→B→O的方向运动,⊙P的半径是$\sqrt{3}$,⊙P运动一圈与△ABC的边相切几次,其中与边AB相切时,点P的坐标为(6,0),(3,3$\sqrt{3}$).
如图,等边三角形OAB的边长为8,点P沿O→A→B→O的方向运动,⊙P的半径是$\sqrt{3}$,⊙P运动一圈与△ABC的边相切几次,其中与边AB相切时,点P的坐标为(6,0),(3,3$\sqrt{3}$).