题目内容
11．（1）计算：（$\frac{1}{2}$）-2-6sin30°-（$\frac{1}{\sqrt{7}-\sqrt{5}}$）0+$\sqrt{2}$+|$\sqrt{2}$-$\sqrt{3}$|（2）解不等式组$\left\{\begin{array}{l}{3x+2≤2（x+3）}\\{\frac{2x-1}{3}＞\frac{x}{2}}\end{array}\right.$，并写出不等式组的整数解．
分析 （1）根据负整数整数幂、零指数幂和特殊角的三角函数值计算；
（2）分别解两个不等式得到x≤4和x＞2，再利用大于小的小于大的取中间得到不等式组的解集，然后确定不等式组的整数解．
解答 解：（1）原式=4-6×$\frac{1}{2}$-1+$\sqrt{2}$+$\sqrt{3}$-$\sqrt{2}$
=$\sqrt{3}$；
（2）$\left\{\begin{array}{l}{3x+2≤2（x+3）①}\\{\frac{2x-1}{3}＞\frac{x}{2}②}\end{array}\right.$，
解①得x≤4，
解②得x＞2，
所以不等式组的解集为2＜x≤4，
所以不等式组的整数解为x=3 或x=4．
点评 本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．也考查了解一元一次不等式．
练习册系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
1．二元一次方程组$\left\{\begin{array}{l}{x+y=4}\\{x-y=2}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ |
2．已知二元一次方程2x-7y=5，用含x的代数式表示y，正确的是（ ）
| A． | $y=\frac{2x+5}{7}$ | B． | $y=\frac{2x-5}{7}$ | C． | $x=\frac{5+7y}{2}$ | D． | $x=\frac{5-7y}{2}$ |
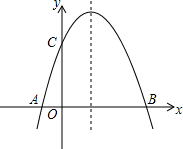已知：二次函数y=ax2+bx+6（a≠0）的图象与x轴交于A、B两点（点A在点B的左侧，点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根．