题目内容
7.m为何值时,关于x的方程(m-$\sqrt{2}$)x${\;}^{{m}^{2}}$-(m+3)x=4x是一元二次方程?并写出该方程中的二次项、一次项、常数项以及各项的系数.分析 直接利用一元二次方程的定义得出m的值,进而得出各项系数.
解答 解:∵关于x的方程(m-$\sqrt{2}$)x${\;}^{{m}^{2}}$-(m+3)x=4x是一元二次方程,
∴m2=2,m-$\sqrt{2}$≠0,
解得:m=-$\sqrt{2}$,
原式可整理为:-2$\sqrt{2}$x2-(-$\sqrt{2}$+7)x=0,
故二次项系数为:-2$\sqrt{2}$,一次项系数为:-(-$\sqrt{2}$+7),常数项为:0.
点评 此题主要考查了一元二次方程的定义,正确得出m的值是解题关键.

练习册系列答案
相关题目
17.方程(x-4)$\sqrt{x-2}$=$\sqrt{2-x}$的解的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数个 |
14.下列图形中是中心对称图形的是( )
| A. |  正三角形 | B. |  正方形 | C. |  等腰梯形 | D. |  正五边形 |
16.若实数x、y满足$\left\{\begin{array}{l}{{x}^{2}+xy+{y}^{2}=7}\\{{x}^{2}-xy+{y}^{2}=3}\end{array}\right.$,则x2014+y2014的值是( )
| A. | 22014+1 | B. | 22014-1 | C. | -22014+1 | D. | -22014-1 |
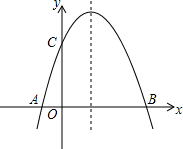 已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧,点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.
已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧,点A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.