题目内容
2.(a+b-c)(-c-a-b)=c2-(a+b)2.分析 利用平方差公式的结构特征判断即可.
解答 解:(a+b-c)(-c-a-b)=c2-(a+b)2.
故答案为:(-c-a-b).
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
12. 在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )
在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )
 在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )
在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
10.若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=3cm,BC=5cm,则矩形EFGH的周长是( )
| A. | 16cm | B. | 12cm | C. | 24cm | D. | 36cm |
7. 如图,已知∠1=65°,则∠A与∠C的度数和为( )
如图,已知∠1=65°,则∠A与∠C的度数和为( )
 如图,已知∠1=65°,则∠A与∠C的度数和为( )
如图,已知∠1=65°,则∠A与∠C的度数和为( )| A. | 65° | B. | 115° | C. | 125° | D. | 无法确定 |
14.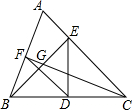 如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )
如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )
 如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )
如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )| A. | 67° | B. | 100° | C. | 113° | D. | 120° |
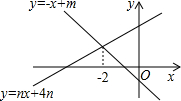 如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式nx+4n>-x+m>0的整数解可能是( )
如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式nx+4n>-x+m>0的整数解可能是( ) 如图,在?ABCD中,对角线AC⊥AB,O为AC的中点,经过点O的直线交AD于E,交BC于F,连结AF、CE,现在添加一个适当的条件,使四边形AFCE是菱形,下列条件:①OE=OA;②EF⊥AC;③AF平分∠BAC;④E为AD中点.正确的有( )个.
如图,在?ABCD中,对角线AC⊥AB,O为AC的中点,经过点O的直线交AD于E,交BC于F,连结AF、CE,现在添加一个适当的条件,使四边形AFCE是菱形,下列条件:①OE=OA;②EF⊥AC;③AF平分∠BAC;④E为AD中点.正确的有( )个.