题目内容
17．抛物线y=$\frac{1}{2}{x}^{2}$，y=-$\frac{1}{2}{x}^{2}$，y=2x2+$\frac{1}{2}$共有的一条性质是（ ）| A． | 开口向上 | B． | 都有一个最高点 | ||
| C． | 对称轴是y轴 | D． | y随x的增大而增大 |
分析 根据二次函数的性质解题．
解答 解：（1）y=$\frac{1}{2}$x2开口向上，对称轴为y轴，有最低点，顶点为原点；
（2）y=-$\frac{1}{2}$x2开口向下，对称轴为y轴，有最高点，顶点为原点；
（3）y=2x2+$\frac{1}{2}$开口向上，对称轴为y轴，有最低点，顶点为（0，$\frac{1}{2}$）；
故选C．
点评 此题考查二次函数的性质，牢记顶点式y=a（x-h）2+k的性质是解答本题的关键．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知抛物线y=ax2-4ax+3与x轴交于A（1，0），B，与y轴交于点C．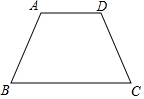
如图，在四边形ABCD中，AD∥BC，AB=CD=6cm，AD=4cm，BC=10cm，求∠D的度数．
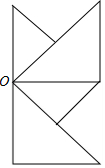以点O为对称中心，画出与如图所示图形成中心对称的图形．