题目内容
2．
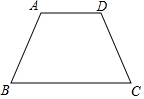如图，在四边形ABCD中，AD∥BC，AB=CD=6cm，AD=4cm，BC=10cm，求∠D的度数．
分析 过A，D分别作AE⊥BC，DF⊥BC，则CF=BE=3，四边形AEFD是矩形，于是得到∠ADF=90°，解直角三角形即可得到结论．
解答 
解：过A，D分别作AE⊥BC，DF⊥BC，
则CF=BE=3，四边形AEFD是矩形，
∴∠ADF=90°，
∴sin∠CDF=$\frac{CF}{CD}$=$\frac{1}{2}$，
∴∠CDF=30°，
∴∠ADC=120°．
点评 本题考查了矩形的判定和性质，解直角三角形，正确的作出辅助线是解题的关键．
练习册系列答案
智能训练练测考系列答案
相关题目
12．下列各式中，计算的结果为负数的是（ ）
| A． | $\root{3}{125}$ | B． | -32 | C． | $\sqrt{16}$ | D． | $\sqrt{\frac{1}{4}}$ |
13．对于二次函数y=-$\frac{1}{2}$（x-4）2+5的图象，有下列说法：①其图象开口向上；②对称轴是直线x=4；③顶点坐标是（-4，5）；④与y轴的交点坐标是（0，3），其中正确的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
17．抛物线y=$\frac{1}{2}{x}^{2}$，y=-$\frac{1}{2}{x}^{2}$，y=2x2+$\frac{1}{2}$共有的一条性质是（ ）
| A． | 开口向上 | B． | 都有一个最高点 | ||
| C． | 对称轴是y轴 | D． | y随x的增大而增大 |
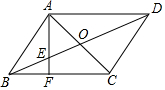如图，平行四边形ABCD中，AC、BD交于点O，E是OB的中点，AE延长线交BC于F，求证：CF=2BF．