题目内容
7.已知⊙O的半径为3,直线m上有一动点P,OP=3,则直线与⊙O的位置关系是相切.分析 直接根据直线与圆的位置关系即可得出结论.
解答 解:∵⊙O的半径为3,直线m上有一动点P,OP=3,
∴直线与⊙O相切.
故答案为:相切.
点评 本题考查的是直线与圆的位置关系,熟知⊙O的半径为r,圆心O到直线l的距离为d,当d=r时,直线l和⊙O相切是解答此题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
12.下列各式中,计算的结果为负数的是( )
| A. | $\root{3}{125}$ | B. | -32 | C. | $\sqrt{16}$ | D. | $\sqrt{\frac{1}{4}}$ |
19. 某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况,如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )
某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况,如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )
 某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况,如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )
某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况,如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为( )| A. | 300米 | B. | 1502米 | C. | 900米 | D. | (300$\sqrt{3}$+300)米 |
17.抛物线y=$\frac{1}{2}{x}^{2}$,y=-$\frac{1}{2}{x}^{2}$,y=2x2+$\frac{1}{2}$共有的一条性质是( )
| A. | 开口向上 | B. | 都有一个最高点 | ||
| C. | 对称轴是y轴 | D. | y随x的增大而增大 |
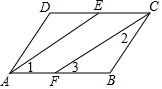 如图,已知∠DAB=∠BCD,AE平分∠DAB,CF平分∠BCD,AE∥CF,试说明∠2=∠3的理由.
如图,已知∠DAB=∠BCD,AE平分∠DAB,CF平分∠BCD,AE∥CF,试说明∠2=∠3的理由. 如图,∠1的同旁内角是∠B、∠C,∠2的内错角是∠C.
如图,∠1的同旁内角是∠B、∠C,∠2的内错角是∠C.