题目内容
1. 已知反比例函数y1=$\frac{k}{x}$和一次函数y=x+b的图象都经过(2,1)
已知反比例函数y1=$\frac{k}{x}$和一次函数y=x+b的图象都经过(2,1)(1)求这两个函数解析式;
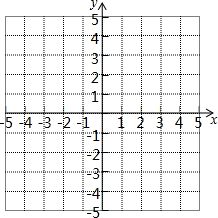
(2)在如图的坐标系中画出两个函数图象(不必列表);
(3)根据图象回答,当y1>y2时,x的取值范围是x<-1或0<x<2.
分析 (1)把(2,1)分别代入反比例函数y1=$\frac{k}{x}$和一次函数y=x+b即可得到结论;
(2)在平面直角坐标系中,画出反比例函数y1=$\frac{k}{x}$和一次函数y=x+b的图象即可;
(3)根据反比例函数y1=$\frac{k}{x}$和一次函数y=x+b的交点坐标即可求得结论.
解答  解:(1)∵反比例函数y1=$\frac{k}{x}$和一次函数y=x+b的图象都经过(2,1),
解:(1)∵反比例函数y1=$\frac{k}{x}$和一次函数y=x+b的图象都经过(2,1),
∴1=$\frac{k}{2}$,1=2+b,
∴k=2,b=-1,
∴反比例函数的解析式为:y=$\frac{2}{x}$,一次函数的解析式为:y=x-1;
(2)如图所示,
(3)由图象知:当x<-1,或0<x<2时,y1>y2,
故答案为:x<-1,或0<x<2.
点评 此题主要考查了反比例函数和一次函数的交点问题,图象性质,待定系数法求解析式,要掌握它们的性质是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
11.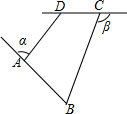 如图,已知四边形ABCD,∠α,∠β分别是∠BAD,∠BCD相邻的补角,且∠B+∠ADC=140°,则∠α+∠β等于( )
如图,已知四边形ABCD,∠α,∠β分别是∠BAD,∠BCD相邻的补角,且∠B+∠ADC=140°,则∠α+∠β等于( )
 如图,已知四边形ABCD,∠α,∠β分别是∠BAD,∠BCD相邻的补角,且∠B+∠ADC=140°,则∠α+∠β等于( )
如图,已知四边形ABCD,∠α,∠β分别是∠BAD,∠BCD相邻的补角,且∠B+∠ADC=140°,则∠α+∠β等于( )| A. | 140° | B. | 170° | C. | 260° | D. | 120° |
16. 课间操时,小华、小军、小刚的位置如图,小军对小刚说,如果我的位置用(0,0)表示,小华的位置用(-2,-1)表示,那么小刚你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图,小军对小刚说,如果我的位置用(0,0)表示,小华的位置用(-2,-1)表示,那么小刚你的位置可以表示成( )
 课间操时,小华、小军、小刚的位置如图,小军对小刚说,如果我的位置用(0,0)表示,小华的位置用(-2,-1)表示,那么小刚你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图,小军对小刚说,如果我的位置用(0,0)表示,小华的位置用(-2,-1)表示,那么小刚你的位置可以表示成( )| A. | (5,4) | B. | (4,3) | C. | (2,2) | D. | (3,4) |
11.在下列四组线段中,能组成直角三角形的是( )
| A. | a=32,b=42,c=52 | B. | a=11,b=12,c=13 | C. | a=9,b=40,c=41 | D. | a:b:c=1:1:2 |
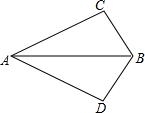 如图,∠ABC=∠ABD,AC=AD,根据AAS定理,要使△ABC≌△ABD,则须补充的一个条件是∠CAB=∠DAB.
如图,∠ABC=∠ABD,AC=AD,根据AAS定理,要使△ABC≌△ABD,则须补充的一个条件是∠CAB=∠DAB.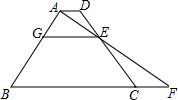 如图,在梯形ABCD中,AD∥BC,AB=CD,过A作AE⊥AB交CD于E,交BC延长线于F,点E恰好是CD的一个三等分点(CE>ED),过E作BC的平行线与AB交于点G.若EG=3,CF=2,则梯形ABCD的面积为12$\sqrt{2}$.
如图,在梯形ABCD中,AD∥BC,AB=CD,过A作AE⊥AB交CD于E,交BC延长线于F,点E恰好是CD的一个三等分点(CE>ED),过E作BC的平行线与AB交于点G.若EG=3,CF=2,则梯形ABCD的面积为12$\sqrt{2}$.