题目内容
9.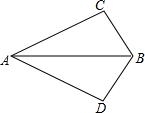 如图,∠ABC=∠ABD,AC=AD,根据AAS定理,要使△ABC≌△ABD,则须补充的一个条件是∠CAB=∠DAB.
如图,∠ABC=∠ABD,AC=AD,根据AAS定理,要使△ABC≌△ABD,则须补充的一个条件是∠CAB=∠DAB.
分析 已知一组角、一对边对应相等,则根据AAS定理,可以添加另一组角相等.
解答 解:需要添加的条件是:∠CAB=∠DAB.
在△ABC与△ABD中,
$\left\{\begin{array}{l}{∠ABC=∠ABD}\\{∠CAB=∠DAB}\\{AC=AD}\end{array}\right.$,
∴△ABC≌△ABD(AAS),
故答案是:∠CAB=∠DAB.
点评 此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.在实数0,$\frac{1}{3}$,$\sqrt{3}$,2.57,$\frac{π}{2}$中无理数的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
20.水库管理人员为掌握水库蓄水情况,需要观测水库水位变化,下表是一周内水位高低的变化情况,用正数表示水位比前一天上升数,用负数表示水位比前一天下降数.
(1)问水库的水位在本周内是上升还是下降,幅度是多少米?
(2)这一周内,哪一天水库的水位最高?哪一天的水位最低?最高水位比最低水位高多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 水位变化(米) | 0.12 | -0.02 | -0.13 | -0.20 | -0.08 | -0.02 | 0.32 |
(2)这一周内,哪一天水库的水位最高?哪一天的水位最低?最高水位比最低水位高多少?
18.已知反比例函数的图象经过点(2,3),则它的图象一定也经过( )
| A. | (-2,-3) | B. | (2,-3) | C. | (-2,3) | D. | (0,0) |
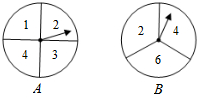 如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字,现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字,现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y). 已知反比例函数y1=$\frac{k}{x}$和一次函数y=x+b的图象都经过(2,1)
已知反比例函数y1=$\frac{k}{x}$和一次函数y=x+b的图象都经过(2,1)