题目内容
4.计算:(1)x•x2•x-2(x≠0)
(2)-t3•(-t)4•(-t)5;
(3)-12017-(-2)-2-($\frac{1}{3}$)-3÷(3.14-π)0
(4)(-2x2)3+x2•x4-(-3x3)2
(5)(a-b)10÷(b-a)3÷(b-a)2
(6)(1$\frac{2}{3}$)2006×(-0.6)2007.
分析 (1)根据同底数幂的乘法法则求出即可;
(2)先算乘方,再根据同底数幂的乘法法则求出即可;
(3)先算乘方,再算除法,最后算加减即可;
(4)先算乘方,再算乘法,最后合并同类项即可;
(5)先变形,再根据同底数幂的除法法则求出即可;
(6)先根据积的乘方进行变形,再求出即可.
解答 解:(1)x•x2•x-2
=x;
(2)-t3•(-t)4•(-t)5
=-t3•t4•(-t5)
=t12;
(3)-12017-(-2)-2-($\frac{1}{3}$)-3÷(3.14-π)0
=-1-$\frac{1}{4}$-27÷1
=-28$\frac{1}{4}$;
(4)(-2x2)3+x2•x4-(-3x3)2
=-8x6+x6-9x6
=-16x6;
(5)(a-b)10÷(b-a)3÷(b-a)2
=(a-b)10÷[-(a-b)3]÷(a-b)2
=-(a-b)5;
(6)(1$\frac{2}{3}$)2006×(-0.6)2007
=[$\frac{5}{3}$×(-$\frac{3}{5}$)]2006×(-$\frac{3}{5}$)
=-$\frac{3}{5}$.
点评 本题考查了整式的混合运算,同底数幂的乘法和除法,零指数幂,负整数指数幂等知识点,能灵活运用知识点进行计算和化简是解此题的关键,注意:运算顺序.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
9.“保护好环境,拒绝冒黑烟”.某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型公交车x辆,完成下表:
(3)若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用最少?最少总费用是多少?
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型公交车x辆,完成下表:
| 数量(辆) | 购买总费用(万元) | 载客总量(万人次) | |
| A型车 | x | 100x | 60x |
| B型车 | 10-x | 150(10-x) | 100(10-x) |
14.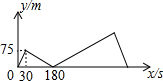 甲、乙两人在直线道路上同起点,同终点,同方向,分别以不同的速度匀速跑步1500m,先到终点的人原地休息,已知甲先出发30s后,乙才出发,甲、乙两人的距离y(m)与甲出发的时间x(s)之间的关系如图所示,下列说法中错误的是( )
甲、乙两人在直线道路上同起点,同终点,同方向,分别以不同的速度匀速跑步1500m,先到终点的人原地休息,已知甲先出发30s后,乙才出发,甲、乙两人的距离y(m)与甲出发的时间x(s)之间的关系如图所示,下列说法中错误的是( )
 甲、乙两人在直线道路上同起点,同终点,同方向,分别以不同的速度匀速跑步1500m,先到终点的人原地休息,已知甲先出发30s后,乙才出发,甲、乙两人的距离y(m)与甲出发的时间x(s)之间的关系如图所示,下列说法中错误的是( )
甲、乙两人在直线道路上同起点,同终点,同方向,分别以不同的速度匀速跑步1500m,先到终点的人原地休息,已知甲先出发30s后,乙才出发,甲、乙两人的距离y(m)与甲出发的时间x(s)之间的关系如图所示,下列说法中错误的是( )| A. | 甲的速度是2.5m/s,乙的速度为3m/s | |
| B. | 乙出发150秒后追上了甲 | |
| C. | 乙到达终点时,甲距终点250m | |
| D. | 甲到达终点比乙晚了70s |
 如图,已知:$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$,求证:∠CAE=∠BAD.
如图,已知:$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$,求证:∠CAE=∠BAD. 如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是14.
如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是14.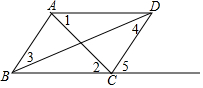 如图,
如图, 如图,将一个长方形纸条折成如图的形状,若已知∠1=130°,则∠2=65°.
如图,将一个长方形纸条折成如图的形状,若已知∠1=130°,则∠2=65°.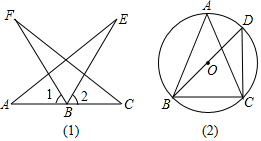 (1)如图(1),AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.
(1)如图(1),AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.