题目内容
14．
如图，已知：$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$，求证：∠CAE=∠BAD．
分析 先根据三组对应边的比相等的两个三角形相似，得出△ABC∽△ADE，进而根据相似三角形的性质，得出∠BAC=∠DAE，即可得到∠CAE=∠BAD．
解答 证明：∵$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$，
∴△ABC∽△ADE，
∴∠BAC=∠DAE，
∴∠BAD+∠DAC=∠DAC+∠CAE，
∴∠CAE=∠BAD．
点评 本题主要考查了相似三角形的判定与性质的运用，解题时注意：三组对应边的比相等的两个三角形相似．
练习册系列答案
相关题目
5．
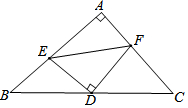如图，在△ABC中，∠A=90°，点D是BC的中点，过点D作DE⊥DF分别AB、AC于点E、F．若BE=1.5，CF=2，则EF的长是（ ）
如图，在△ABC中，∠A=90°，点D是BC的中点，过点D作DE⊥DF分别AB、AC于点E、F．若BE=1.5，CF=2，则EF的长是（ ）| A． | 2.4 | B． | 2.5 | C． | 3 | D． | 3.5 |
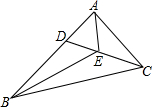在△ABC中，点D为AB边上一点，BD=2AD，点E为CD的中点，若S△ADE=2，则S△ABC=12．