题目内容
13.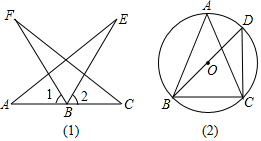 (1)如图(1),AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.
(1)如图(1),AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.(2)如图(2),⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BD=2,连接CD,求BC的长.
分析 (1)由∠1=∠2,利用等式的性质得到夹角相等,利用SAS即可得证;
(2)利用同弧所对的圆周角相等求出∠D的度数,再由BD为圆O的直径,得到∠BCD为直角,进而得出三角形BCD为等腰直角三角形,根据BD的长求出BC的长即可.
解答 证明:(1)∵∠1=∠2,
∴∠1+∠FBE=∠2+∠FBE,即∠ABE=∠CBF,
∵AB=CB,BE=BF,
∴△ABE≌△CBF(SAS);
(2)在圆O中,∵∠A=45°,$\widehat{BC}$=$\widehat{BC}$,
∴∠D=45°,
∵BD为圆的直径,
∴∠BCD=90°,
∴△BCD是等腰直角三角形,
∴BC=BD•sin45°,
∵BD=2,
∴BC=$\sqrt{2}$.
点评 此题考查了三角形的外接圆与外心,以及全等三角形的判定与性质,熟练掌握圆周角定理及全等三角形的判定方法是解本题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
8.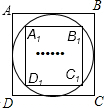 如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )
如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )
 如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )
如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )| A. | ($\frac{\sqrt{2}}{2}$)n | B. | ($\frac{1}{2}$)n | C. | ($\frac{\sqrt{3}}{2}$)n | D. | ($\frac{3}{4}$)n |
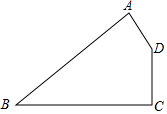 如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500$\sqrt{2}$米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?
如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500$\sqrt{2}$米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?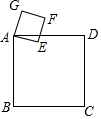 如图,已知正方形ABCD与正方形AEFG的边长分别为4cm,1cm,若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为3$\sqrt{2}$cm.
如图,已知正方形ABCD与正方形AEFG的边长分别为4cm,1cm,若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为3$\sqrt{2}$cm. 如图中四边形ABCD是由两块完全重合的三角板拼成的,且AB=2,∠ACD=90°,∠DAC=30°,开始将一把直尺边EF放在与AC重叠的位置,再由此将直尺绕着AC中点P顺时针旋转角β,当直尺边EF与直线BD重叠时旋转就停止,在旋转过程中EF分别与线段BC、AD交于E、F.
如图中四边形ABCD是由两块完全重合的三角板拼成的,且AB=2,∠ACD=90°,∠DAC=30°,开始将一把直尺边EF放在与AC重叠的位置,再由此将直尺绕着AC中点P顺时针旋转角β,当直尺边EF与直线BD重叠时旋转就停止,在旋转过程中EF分别与线段BC、AD交于E、F.