题目内容
14.求证:等腰三角形两腰上的中线的交点到底边两个端点的距离相等.分析 作出图形,然后写出已知、求证,再根据线段中点的定义求出BD=CE,然后利用“边角边”证明△BCD和△CBE全等,根据全等三角形对应角相等可得∠BCD=∠CBE,再根据等角对等边证明即可.
解答 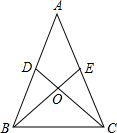 已知:如图,AB=AC,△ABC的中线BD、CE相交于点O,
已知:如图,AB=AC,△ABC的中线BD、CE相交于点O,
求证:BO=CO;
证明:∵BD、CE是△ABC的中线,
∴BD=$\frac{1}{2}$AB,CE=$\frac{1}{2}$AC,
∵AB=AC,
∴BD=CE,
∵AB=AC,
∴∠ABC=∠ACB,
在△BCD和△CBE中,$\left\{\begin{array}{l}{BD=CE}\\{∠ABC=∠ACB}\\{BC=CB}\end{array}\right.$,
∴△BCD≌△CBE(SAS),
∴∠BCD=∠CBE,
∴BO=CO.
点评 本题考查了全等三角形的判定与性质,等腰三角形的性质,文字叙述性命题的证明方法为作出图形,然后写出已知、求证、证明,要熟练掌握,本题确定出全等三角形是解题的关键.

练习册系列答案
相关题目
2.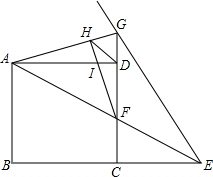 如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )
如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )
①GE+GD=BE;②DG=DF;③AC-2HD=$\sqrt{2}$DF;④当CE=BC=2时,FG=$\frac{5}{3}$.
 如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )
如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )①GE+GD=BE;②DG=DF;③AC-2HD=$\sqrt{2}$DF;④当CE=BC=2时,FG=$\frac{5}{3}$.
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
2.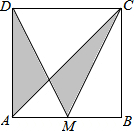 如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
 如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
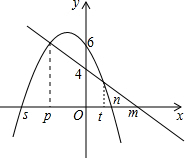 如图,已知:一次函数图象y1=kx+d与x轴交于点(m,0),与y轴交于(0,4),二次函数y2=ax2+bx+c图象与x轴交于点(s,0)和(n,0),与y轴交于(0,6),且两个函数图象交点的横坐标分别为p、t,则y3=ax2+(b-k)x+2的图象与x轴的交点坐标是(p,0)和(t,0).
如图,已知:一次函数图象y1=kx+d与x轴交于点(m,0),与y轴交于(0,4),二次函数y2=ax2+bx+c图象与x轴交于点(s,0)和(n,0),与y轴交于(0,6),且两个函数图象交点的横坐标分别为p、t,则y3=ax2+(b-k)x+2的图象与x轴的交点坐标是(p,0)和(t,0).
 如图,BD:DC=3:5,F是AD中点,那么S△AEF:S△FDC=3:13..
如图,BD:DC=3:5,F是AD中点,那么S△AEF:S△FDC=3:13.. 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转20°.
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转20°. 如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.有下列四个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④$\frac{{S}_{△ACD}}{{S}_{四边形BCDE}}$=$\frac{1}{6}$.其中正确的结论是①②(填写正确结论的序号).
如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接DF,EF,∠ACB=90°,∠ABC=30°.有下列四个结论:①AC⊥DF;②四边形BCDF为平行四边形;③DA+DF=BE;④$\frac{{S}_{△ACD}}{{S}_{四边形BCDE}}$=$\frac{1}{6}$.其中正确的结论是①②(填写正确结论的序号).