题目内容
已知多项式x3+ax2+bx-4能够被多项式x2+3x-4整除，求a，b的值．
考点：整式的除法
专题：计算题
分析：根据题意设x3+ax2+bx-4=（x2+3x-4）（x+m），右边利用多项式乘多项式法则计算，利用多项式相等的条件求出a与b的值即可．
解答：解：∵多项式x3+ax2+bx-4能够被多项式x2+3x-4整除，
∴x3+ax2+bx-4=（x2+3x-4）（x+m）=x3+（m+3）x2+（3m-4）x-4m，
可得a=m+3，b=3m-4，-4m=-1，
解得：m=1，a=4，b=-1．
∴x3+ax2+bx-4=（x2+3x-4）（x+m）=x3+（m+3）x2+（3m-4）x-4m，
可得a=m+3，b=3m-4，-4m=-1，
解得：m=1，a=4，b=-1．
点评：此题考查了整式的除法，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
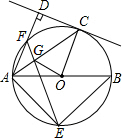如图，在半径为5的⊙O中，AB是直径，点C是⊙O上一点，AD和过点C的切线互相垂直，垂足为D．
．求该二次函数的表达式．
如图，矩形ABCD中，E，F分别在BC，AD上，矩形ABCD∽矩形ECDF，