题目内容
将下列多项式分解因式．
（1）2ma2-8mb2
（2）a3-2a2b+ab2
（3）a2（x-y）+b2（y-x）
（4）（3x-y）2-（x-3y）2．
（1）2ma2-8mb2
（2）a3-2a2b+ab2
（3）a2（x-y）+b2（y-x）
（4）（3x-y）2-（x-3y）2．
考点：提公因式法与公式法的综合运用
专题：计算题
分析：（1）原式提取公因式，再利用平方差公式分解即可；
（2）原式提取公因式，再利用完全平方公式分解即可；
（3）原式变形后，提取公因式，再利用平方差公式分解即可；
（4）原式利用平方差公式分解即可．
（2）原式提取公因式，再利用完全平方公式分解即可；
（3）原式变形后，提取公因式，再利用平方差公式分解即可；
（4）原式利用平方差公式分解即可．
解答：解：（1）原式=2m（a2-b2）=2m（a+b）（a-b）；
（2）原式=a（a2-2ab+b2）=a（a-b）2；
（3）原式=a2（x-y）-b2（x-y）=（x-y）（a+b）（a-b）；
（4）原式=（3x-y+x-3y）（3x-y-x+3y）=8（x+y）（x-y）．
（2）原式=a（a2-2ab+b2）=a（a-b）2；
（3）原式=a2（x-y）-b2（x-y）=（x-y）（a+b）（a-b）；
（4）原式=（3x-y+x-3y）（3x-y-x+3y）=8（x+y）（x-y）．
点评：此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
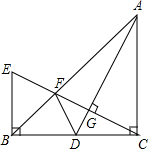如图，在△ABC中，∠BCA=90°，CA=CB，AD为BC边上的中线，CG⊥AD于G，交AB于F，过点B作B C的垂线交CG于E．现有下列结论：①△ADC≌△CEB；②AB=CE；③∠ADC=∠BDF；④F为EG中点．其中结论正确的个数为（ ）
如图，已知△ABC是边长为6的等边三角形，点O在边AB上，⊙O过点B且分别与AB，BC相交于点D、E，过点E的切线与AC相交于点F．