题目内容
 如图,矩形ABCD中,E,F分别在BC,AD上,矩形ABCD∽矩形ECDF,
如图,矩形ABCD中,E,F分别在BC,AD上,矩形ABCD∽矩形ECDF,且AB=2,S矩形ABCD=3S矩形ECDF.试求S矩形ABCD.
考点:相似多边形的性质
专题:
分析:根据矩形的面积求出AD=4DF,然后根据相似多边形的对应边成比例列式求出AD,然后根据矩形的面积公式列式计算即可得解.
解答:解:∵AB=2,
∴CD=AB=2,
∵S矩形ABCD=3S矩形ECDF,
∴AF=3DF,
∴AD=4DF,
∵矩形ABCD∽矩形ECDF,
∴
=
,
即
=
,
∴4DF2=4,
解得DF=1,
∴AD=4×1=4,
∴S矩形ABCD=AB•AD=2×4=8.
∴CD=AB=2,
∵S矩形ABCD=3S矩形ECDF,
∴AF=3DF,
∴AD=4DF,
∵矩形ABCD∽矩形ECDF,
∴
| AB |
| DF |
| AD |
| CD |
即
| 2 |
| DF |
| AD |
| 2 |
∴4DF2=4,
解得DF=1,
∴AD=4×1=4,
∴S矩形ABCD=AB•AD=2×4=8.
点评:本题考查了相似多边形的性质,矩形的性质,利用矩形的面积求出AD=4DF是解题的关键.

练习册系列答案
相关题目
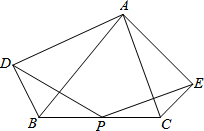 如图,以△ABC的AB、AC边为斜边向外作Rt△ABD和Rt△ACE,且使∠ABD=∠ACE=α,P是BC中点,
如图,以△ABC的AB、AC边为斜边向外作Rt△ABD和Rt△ACE,且使∠ABD=∠ACE=α,P是BC中点,