题目内容
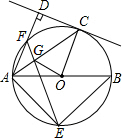 如图,在半径为5的⊙O中,AB是直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
如图,在半径为5的⊙O中,AB是直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D.(1)求证:AC平分∠DAB;
(2)若点E是半圆的中点,AD和⊙O交于点F,AF=6,连接FE,交AC于点G,连结OG,求S△AOG.
考点:切线的性质,勾股定理,切线长定理
专题:
分析:(1)由CD与⊙O相切,AD⊥CD,可得AD∥OC,继而可得∠CAD=∠CAO,即AC平分∠DAB;
(2)首先连接BF,过点G分别作GP⊥AB,GM⊥AD,GN⊥FB,垂足为点P、M、N,可证得四边形MGNF是矩形,继而可得矩形MGFN是正方形,然后设设MF=a,则由切线长定理得:AM=AP=6-a,BN=BP=8-a,由AP+BP=AB,可得:(6-a)+(8-a)=10,继而求得答案.
(2)首先连接BF,过点G分别作GP⊥AB,GM⊥AD,GN⊥FB,垂足为点P、M、N,可证得四边形MGNF是矩形,继而可得矩形MGFN是正方形,然后设设MF=a,则由切线长定理得:AM=AP=6-a,BN=BP=8-a,由AP+BP=AB,可得:(6-a)+(8-a)=10,继而求得答案.
解答:(1)证明:∵CD与⊙O相切,
∴OC⊥CD,
∴∠OCD=90°,
∵AD⊥CD.
∴∠ADC=90°,
∴∠OCD+∠ADC=180°,
∴AD∥OC,
∴∠ACO=∠CAD,
∵OA、OC为⊙O半径,
∴OA=OC,
∴∠ACO=∠CAO,
∴∠CAD=∠CAO,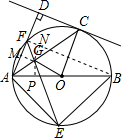
∴AC平分∠DAB;
(2)解:连接BF,过点G分别作GP⊥AB,GM⊥AD,GN⊥FB,垂足为点P、M、N,
∵AB是⊙O直径,半径为5,
∴∠AFB=90°,AB=10,
在Rt△AFB中由勾股定理得:BF=8,
∵GM⊥AD,GN⊥FB,
∴∠GMF=∠GNF=∠AFB=90°,
∴四边形MGNF是矩形,
∵点E是半圆的中点,
∴∠AFE=∠BFE,
∴EF平分∠AFB,
∴GM=GN,
∴矩形MGFN是正方形,
∴MF=FN=MG=GN,
又∵AC平分∠DAB,
∴点G为⊙O的内心,
又∵GP⊥AB,GM⊥AD,GN⊥FB,
∴点P、M、N为△ABF与内切圆⊙G的切点,且GP=GM=GN,
∴设MF=a,则由切线长定理得:AM=AP=6-a,BN=BP=8-a,
由AP+BP=AB,可得:(6-a)+(8-a)=10,
解得:a=2,
∴FM=GP=2,
∴S△AOG=
OA•GP=
×5×2=5.
∴OC⊥CD,
∴∠OCD=90°,
∵AD⊥CD.
∴∠ADC=90°,
∴∠OCD+∠ADC=180°,
∴AD∥OC,
∴∠ACO=∠CAD,
∵OA、OC为⊙O半径,
∴OA=OC,
∴∠ACO=∠CAO,
∴∠CAD=∠CAO,

∴AC平分∠DAB;
(2)解:连接BF,过点G分别作GP⊥AB,GM⊥AD,GN⊥FB,垂足为点P、M、N,
∵AB是⊙O直径,半径为5,
∴∠AFB=90°,AB=10,
在Rt△AFB中由勾股定理得:BF=8,
∵GM⊥AD,GN⊥FB,
∴∠GMF=∠GNF=∠AFB=90°,
∴四边形MGNF是矩形,
∵点E是半圆的中点,
∴∠AFE=∠BFE,
∴EF平分∠AFB,
∴GM=GN,
∴矩形MGFN是正方形,
∴MF=FN=MG=GN,
又∵AC平分∠DAB,
∴点G为⊙O的内心,
又∵GP⊥AB,GM⊥AD,GN⊥FB,
∴点P、M、N为△ABF与内切圆⊙G的切点,且GP=GM=GN,
∴设MF=a,则由切线长定理得:AM=AP=6-a,BN=BP=8-a,
由AP+BP=AB,可得:(6-a)+(8-a)=10,
解得:a=2,
∴FM=GP=2,
∴S△AOG=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了切线的性质、正方形的判定与性质、切线长定理以及内切圆的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 二次函数y=a(x-h)2的图象如图,已知a=
二次函数y=a(x-h)2的图象如图,已知a= 在平面直角坐标系xOy中,A(0,4),B(2,0),C(5,1),D(2,5).
在平面直角坐标系xOy中,A(0,4),B(2,0),C(5,1),D(2,5).