题目内容
10．若m2+m-1=0，则m3+2m2+2017的值为（ ）| A． | 2016 | B． | 2017 | C． | 2018 | D． | 2019 |
分析 把m2+m-1=0化为m2=1-m，代入原式计算即可．
解答 解：∵m2+m-1=0，
∴m2=1-m，
∴原式=m（1-m）+2m2+2017
=m-m2+2m2+2017
=m2+m+2017
=2018，
故选：C．
点评 本题考查的是因式分解的应用，把已知等式进行正确的变形是解题的关键．
练习册系列答案
相关题目
如图，方格纸中每个小正方形的边长都是1个单位长度，△ABC的三个顶点A（-4，4），B（0，6），C（0，2）．
已知，如图，∠1=∠2，AB=AE，∠ACB=2∠B．求证：
18．$\sqrt{9}+\sqrt{16}$的值是（ ）
| A． | 7 | B． | -1 | C． | 1 | D． | -7 |
15．下列各数化简后与|3|相等的是（ ）
| A． | 3-1 | B． | （-1）3 | C． | |-3| | D． | -（-$\frac{1}{3}$） |
2．若a=355，b=444，c=533，则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | a＞c＞b | C． | c＞b＞a | D． | b＞a＞c |
19．若方程组$\left\{\begin{array}{l}{3x+2y=m+2}\\{2x+3y=m}\end{array}\right.$的解x与y的和为0，则m的值为（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | 2 |
20．
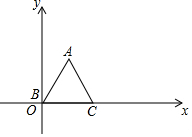已知等边△ABC，顶点B（0，0），C（2，0），规定把△ABC先沿x轴绕着点C顺时针旋转，使点A落在x轴上，称为一次变换，再沿x轴绕着点A顺时针旋转，使点B落在x轴上，称为二次变换，…经过连续2017次变换后，顶点A的坐标是（ ）
已知等边△ABC，顶点B（0，0），C（2，0），规定把△ABC先沿x轴绕着点C顺时针旋转，使点A落在x轴上，称为一次变换，再沿x轴绕着点A顺时针旋转，使点B落在x轴上，称为二次变换，…经过连续2017次变换后，顶点A的坐标是（ ）| A． | （4033，$\sqrt{3}$） | B． | （4033，0） | C． | （4036，$\sqrt{3}$） | D． | （4036，0） |