题目内容
11.在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出2个小球,两球恰好是一个黄球和一个红球的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两球恰好是一个黄球和一个红球的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有12种等可能的结果,两球恰好是一个黄球和一个红球的有6种情况,
∴两球恰好是一个黄球和一个红球的为:$\frac{6}{12}$=$\frac{1}{2}$.
故选A.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
2.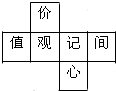 一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )
一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )
 一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )
一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )| A. | 记 | B. | 观 | C. | 心 | D. | 间 |
19. 小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
 小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
3.学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
| 选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
| 甲 | 85 | 78 | 85 | 73 |
| 乙 | 73 | 80 | 82 | 83 |
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
20.已知∠α=35°,那么∠α的余角等于( )
| A. | 35° | B. | 55° | C. | 65° | D. | 145° |
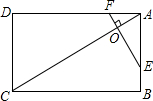 如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.
如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.