题目内容
12.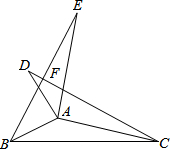 如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=150°,则∠EFC的度数为60°.
如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=150°,则∠EFC的度数为60°.
分析 先根据三角形内角和与翻折变换的特点求得∠EBC+∠DCB=60°,再根据三角形的一个外角等于和它不相邻的两个内角的和得∠EFC=60°.
解答 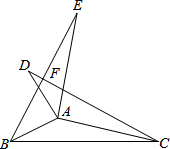 解:∵∠BAC=150°,
解:∵∠BAC=150°,
∴∠ABC+∠ACB=30°,
∵∠EBA=∠ABC,∠DCA=∠ACB,
∴∠EBA+∠ABC+∠DCA+∠ACB=2(∠ABC+∠ACB)=60°,即∠EBC+∠DCB=60,
∴∠EFC=60°.
故答案为:60°.
点评 此题主要考查了折叠的性质和三角形内角和定理的综合运用,巧妙运用三角形的外角的性质“三角形的一个外角等于和它不相邻的两个内角的和”是解决问题的关键.

练习册系列答案
相关题目
2.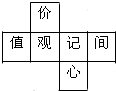 一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )
一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )
 一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )
一个正方体的每个面都有一个汉字,其展开图如图所示,那么在该正方体中和“值”字相对的字是( )| A. | 记 | B. | 观 | C. | 心 | D. | 间 |
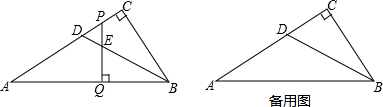
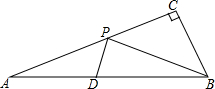 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=2,点D是AB的中点,点P是线段AC上的动点,连接PB,PD,将△BPD沿直线PD翻转,得到△B′PD与△APD重叠部分的面积是△ABP面积的$\frac{1}{4}$时,AP=6-$\sqrt{6}$或$\sqrt{10}$.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=2,点D是AB的中点,点P是线段AC上的动点,连接PB,PD,将△BPD沿直线PD翻转,得到△B′PD与△APD重叠部分的面积是△ABP面积的$\frac{1}{4}$时,AP=6-$\sqrt{6}$或$\sqrt{10}$.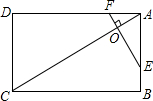 如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.
如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.