题目内容
16.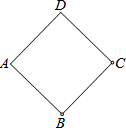 如图,正方形ABCD,边长AB=2.
如图,正方形ABCD,边长AB=2.(1)画出正方形ABCD绕A点顺时针旋转45°后的正方形AB′C′D′;
(2)若CB与C′D′相交于点E,求四边形ABED′的面积.
分析 (1)根据要求画出图形即可;
(2)首先求出△D′EC的直角边,再分别计算△ABC和△D′EC的面积作差即可.
解答 解:(1)如右图所示:
(2)∵正方形的边长为1,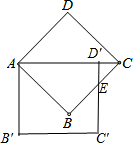
∴AC=$\sqrt{2}$,
∵AD′=AD=1,
∴D′C=$\sqrt{2}$-1,
∵C′D′⊥AC
∴D′E=D′C=$\sqrt{2}$-1,
∴S四边形ABED′=S△ABC-S△D′EC
=$\frac{1}{2}$×12-$\frac{1}{2}$×($\sqrt{2}$-1)2
=$\sqrt{2}$-1.
点评 本题主要考查了图形的旋转变换、勾股定理以及图形面积计算的综合运用,难度不大,关键是做出图形发现四边形面积的分解方法.

练习册系列答案
相关题目
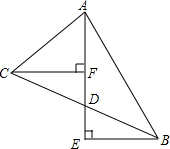 如图,BE⊥AE于E,CF⊥AE于F,D是EF的中点,求证:CD=BD.
如图,BE⊥AE于E,CF⊥AE于F,D是EF的中点,求证:CD=BD.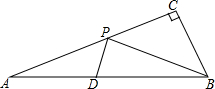 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=2,点D是AB的中点,点P是线段AC上的动点,连接PB,PD,将△BPD沿直线PD翻转,得到△B′PD与△APD重叠部分的面积是△ABP面积的$\frac{1}{4}$时,AP=6-$\sqrt{6}$或$\sqrt{10}$.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=2,点D是AB的中点,点P是线段AC上的动点,连接PB,PD,将△BPD沿直线PD翻转,得到△B′PD与△APD重叠部分的面积是△ABP面积的$\frac{1}{4}$时,AP=6-$\sqrt{6}$或$\sqrt{10}$.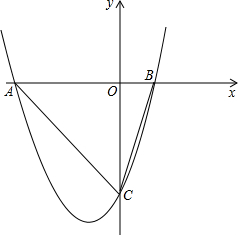 已知抛物线y=x2+2x-3与x轴交于A,B(点A在点B的左侧)两单,与y轴交于点C.
已知抛物线y=x2+2x-3与x轴交于A,B(点A在点B的左侧)两单,与y轴交于点C.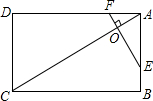 如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.
如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.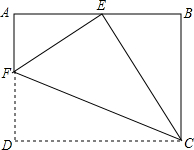 如图,将一张矩形纸片ABCD沿CF折叠,使点D与AB的中点E重合,求$\frac{AF}{FD}$.
如图,将一张矩形纸片ABCD沿CF折叠,使点D与AB的中点E重合,求$\frac{AF}{FD}$.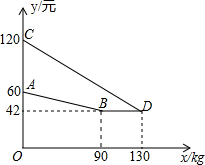 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.