题目内容
11.某班同学在一次综合实践活动中,对本县居民参加“全民医保”情况进行了调查,同学们利用节假日随机调查了3000人,其中参加B,C类医保人数总和是参加A,D类医保人数总和的$\frac{7}{3}$倍.对调查结果进行了统计分析.绘制出两幅不完整的统计图.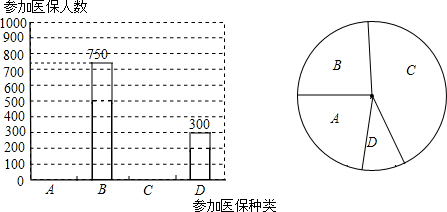
(注:图中A表示城镇职工基本医疗保险;B表示城镇居民基本医疗保险;C表示“新型农村合作医疗”;D表示其他情况)
(1)补全条形图;
(2)在本次调查中,B类人数占被调查人数的百分比为25%,扇形统计图C区域所对应的圆心角大小为162°;
(3)据了解,国家对B类人员每人每年补助200元,若该县人口数约为100万,请估计该县B类人员每年享受国家补助共多少元?
分析 (1)设参加A类医保人数为x人,则参加C类医保人数为(1950-x)人,根据:B类人数+C类人数=$\frac{7}{3}$×(A类人数+D类人数),列方程求解可得;
(2)用B表示的“城镇居民基本医疗保险”的人数÷这次调查的总人数可得B类人数占被调查人数的百分比,C类人数占总人数比例乘以360°可得圆心角度数;
(3)该县B类人员每年享受国家补助的总钱数=国家对B类人员每人每年补助的钱数×100×B类人员所占的百分比.
解答 解:(1)设参加A类医保人数为x人,则参加C类医保人数为:3000-(x+750+300)=1950-x(人),
根据题意,得:750+1950-x=$\frac{7}{3}$(x+300),
解得:x=600,
故参加A类医保人数为600人,参加C类医保人数为:1950-600=1350人,
补全统计图如下:
(2)750÷3000=25%,即在本次调查中,B类人数占被调查人数的百分比为25%.
C区域的圆心角为:$\frac{1350}{3000}$×360°=162°;
(3)200×100×25%=5000(万元).
答:该县B类人员每年享受国家补助共5000万元;
故答案为:(2)25%,162°.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 如图,三角形ABC的面积是288平厘米,3BD=BC,E是AD的中点,EF=2FC,求阴影部分的面积.
如图,三角形ABC的面积是288平厘米,3BD=BC,E是AD的中点,EF=2FC,求阴影部分的面积.