题目内容
14. 如图,点A在y=$\frac{1}{x}$双曲线上,点B在y=$\frac{3}{x}$双曲线上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为2.
如图,点A在y=$\frac{1}{x}$双曲线上,点B在y=$\frac{3}{x}$双曲线上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为2.
分析 延长BA交y轴于E点,如图,利用反比例函数的比例系数k的几何意义得到S矩形ADOE=1,S矩形BEOC=3,然后求它们的差即可.
解答  解:延长BA交y轴于E点,如图,
解:延长BA交y轴于E点,如图,
∵四边形ABCD为矩形,
∴S矩形ADOE=1,S矩形BEOC=3,
∴S矩形ABCD=S矩形BEOC-S矩形ADOE=3-1=2.
故答案为2.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
 如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
9.如图,字母B所代表的正方形的面积是( )


| A. | 12 | B. | 144 | C. | 13 | D. | 194 |
 如图,A,B是4×4网格上的两个格点,在格点中任意放置点C,与点A,点B恰好围成等腰三角形的概率是$\frac{9}{25}$.
如图,A,B是4×4网格上的两个格点,在格点中任意放置点C,与点A,点B恰好围成等腰三角形的概率是$\frac{9}{25}$. 如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH为矩形,∠ADC+∠BCD应为90度.
如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH为矩形,∠ADC+∠BCD应为90度.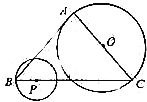 如图,在△ABC中,AB=AC=10,BC=12,点P为BC边上一动点,如果以P为圆心,BP为半径的圆P与以AC为直径的圆O相交,那么点P离开点B的距离BP的取值范围是$\frac{18}{7}$<BP<9.
如图,在△ABC中,AB=AC=10,BC=12,点P为BC边上一动点,如果以P为圆心,BP为半径的圆P与以AC为直径的圆O相交,那么点P离开点B的距离BP的取值范围是$\frac{18}{7}$<BP<9.