题目内容
13. 如图,在直角坐标系中,已知点B(0,6),O(0,0),D(8,0)和点C都在⊙A上,则sin∠BCO=$\frac{3}{5}$.
如图,在直角坐标系中,已知点B(0,6),O(0,0),D(8,0)和点C都在⊙A上,则sin∠BCO=$\frac{3}{5}$.
分析 连接BD,根据勾股定理得到BD,根据三角函数的概念即可得到答案.
解答  解:连接BD,∵B(0,6),D(8,0),
解:连接BD,∵B(0,6),D(8,0),
∴OB=6,OD=8,
∴BD=10,
∵∠BCO=∠D,
在Rt△BDO中,sin∠D=$\frac{OB}{BD}=\frac{6}{10}$=$\frac{3}{5}$,
∴sin∠BCO=$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 本题考查的是圆周角定理和解直角三角形的知识,掌握同弧所对的圆周角相等和锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
18.下列式子中,错误的是( )
| A. | $\sqrt{2}$×$\sqrt{8}$=4 | B. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | C. | $\sqrt{\frac{4}{3}}$=$\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{4\sqrt{18}}{2\sqrt{6}}$=2$\sqrt{3}$ |
5. 如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
 如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
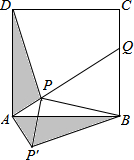 如图,点P是正方形ABCD内一点,PA=1,PB=2$\sqrt{2}$,PD=$\sqrt{10}$,将△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,PA=1,PB=2$\sqrt{2}$,PD=$\sqrt{10}$,将△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.