题目内容
20.在Rt△ABC中,∠C=90°,AB=10,BC=6,则AC的长是( )| A. | 8 | B. | 4$\sqrt{34}$ | C. | 64 | D. | 16 |
分析 直接根据勾股定理进行解答即可.
解答 解:∵在Rt△ABC中,∠C=90°,AB=10,BC=6,
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=$\sqrt{{10}^{2}-{6}^{2}}$=8.
故选A.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
2.如图,AB∥CD,点E在BC上,且CD=CE,∠D=72°,则∠B的度数为( )


| A. | 36° | B. | 68° | C. | 22° | D. | 16° |
5. 如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
 如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )
如图,四边形ABCD是正方形,点E在BC上,△ABE绕正方形的中心经顺时针旋转后与△DAF重合,则旋转角度是( )| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
9.如图,字母B所代表的正方形的面积是( )


| A. | 12 | B. | 144 | C. | 13 | D. | 194 |
10.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{3{a}^{2}}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{27}$ | D. | $\sqrt{35}$ |
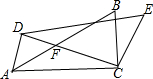 如图,△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕点C按顺时针方向旋转,旋转角为α(0°<α<90°),得到△DEC,设CD交AB于点F,连接AD,当α=40°时,AD=AF.
如图,△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕点C按顺时针方向旋转,旋转角为α(0°<α<90°),得到△DEC,设CD交AB于点F,连接AD,当α=40°时,AD=AF. 如图,半径为2cm的圆O与地面相切于点B,圆周上一点A距地面高为(2+$\sqrt{3}$)cm,圆O沿地面BC方向滚动,当点A第一次接触地面时,圆O在地面上滚动的距离为$\frac{5π}{3}$cm.
如图,半径为2cm的圆O与地面相切于点B,圆周上一点A距地面高为(2+$\sqrt{3}$)cm,圆O沿地面BC方向滚动,当点A第一次接触地面时,圆O在地面上滚动的距离为$\frac{5π}{3}$cm.