题目内容
15．
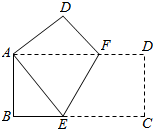如图，将一个边长分别为4cm、8cm的矩形纸片ABCD折叠，使C点与A点重合，则EB的长是3cm．
分析 设BE=x，则CE=AE=8-x，再由勾股定理求出x的值即可．
解答 解：设BE=x，则CE=AE=8-x，
在Rt△ABE中，AB2+BE2=AE2，即42+x2=（8-x）2，解得x=3cm．
故答案为：3cm．
点评 本题考查的是翻折变换，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解答此题的关键．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
5．
如图，四边形ABCD是正方形，点E在BC上，△ABE绕正方形的中心经顺时针旋转后与△DAF重合，则旋转角度是（ ）
如图，四边形ABCD是正方形，点E在BC上，△ABE绕正方形的中心经顺时针旋转后与△DAF重合，则旋转角度是（ ）| A． | 120° | B． | 90° | C． | 60° | D． | 45° |
如图，在四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点，要使四边形EFGH为矩形，∠ADC+∠BCD应为90度．
10．下列二次根式中，最简二次根式是（ ）
| A． | $\sqrt{3{a}^{2}}$ | B． | $\sqrt{\frac{1}{3}}$ | C． | $\sqrt{27}$ | D． | $\sqrt{35}$ |
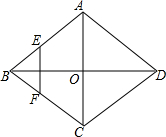如图，菱形ABCD的对角线AC，BD相交于O点，E，F分别是AB，BC边上的中点，连接EF，若EF=$\sqrt{3}$，BD=4，则菱形ABCD的面积为4$\sqrt{3}$．
7．如图，已知AB∥CD，∠1=60°，则∠2=（ ）
| A． | 60° | B． | 100° | C． | 120° | D． | 130° |
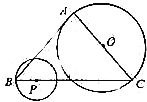如图，在△ABC中，AB=AC=10，BC=12，点P为BC边上一动点，如果以P为圆心，BP为半径的圆P与以AC为直径的圆O相交，那么点P离开点B的距离BP的取值范围是$\frac{18}{7}$＜BP＜9．