题目内容
7.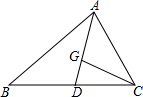 如图,在△ABC中,G是重心,点D是BC的中点,若△ABC的面积为6cm2,则△CGD的面积为1cm2.
如图,在△ABC中,G是重心,点D是BC的中点,若△ABC的面积为6cm2,则△CGD的面积为1cm2.
分析 由于点D是BC的中点,则根据三角形面积公式得到S△ACD=$\frac{1}{2}$S△ABC=3,再利用重心性质得到AG:GD=2:1,然后再利用三角形面积公式可计算出S△CGD=$\frac{1}{3}$S△ACD=1(cm2).
解答 解:∵点D是BC的中点,
∴BD=CD,
∴S△ACD=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×6=3,
∵G是重心,
∴AG:GD=2:1,
∴S△CGD=$\frac{1}{3}$S△ACD=$\frac{1}{3}$×3=1(cm2).
故答案为1.
点评 本题考查了三角形重心:三角形的重心是三角形三边中线的交点.重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查了三角形面积公式.

练习册系列答案
相关题目
15.现定义一种新运算:a※b=b2-ab,如:1※2=22-1×2=2,则(-1※2)※3等于( )
| A. | -9 | B. | -6 | C. | 6 | D. | 9 |
 在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以$\sqrt{2}$cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒,则t=6秒时,S1=2S2.
在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以$\sqrt{2}$cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒,则t=6秒时,S1=2S2.