题目内容
18.计算.(1)$\frac{xy(x+y)}{{(x-y)}^{2}}$•$\frac{x-y}{xy{+y}^{2}}$
(2)${(\sqrt{3}-1)}^{0}$+|-3|-${(\frac{1}{2})}^{2}$+$\sqrt{4}$.
分析 (1)根据分式的乘法进行计算,分子,分母进行约分,即可解答;
(2)先算乘方,再算加减,即可解答.
解答 解:(1)原式=$\frac{xy(x+y)}{(x-y)^{2}}•\frac{x-y}{y(x+y)}$=$\frac{x}{x-y}$.
(2)原式=1+3-$\frac{1}{4}$+2=6-$\frac{1}{4}$=$\frac{23}{4}$.
点评 本题考查了分式的乘法和有理数的混合运算,加减本题的关键是注意运算顺序.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
13.若方程$\frac{3-2x}{x-3}$+$\frac{2+mx}{3-x}$=-1无解,则m的值是( )
| A. | -1 | B. | 3 | C. | -1或3 | D. | -1或-$\frac{5}{3}$ |
8.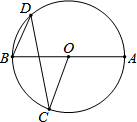 如图,AB是⊙O的直径,C、D是圆上两点,∠BOC=70°,则∠D等于( )
如图,AB是⊙O的直径,C、D是圆上两点,∠BOC=70°,则∠D等于( )
 如图,AB是⊙O的直径,C、D是圆上两点,∠BOC=70°,则∠D等于( )
如图,AB是⊙O的直径,C、D是圆上两点,∠BOC=70°,则∠D等于( )| A. | 25° | B. | 35° | C. | 55° | D. | 70° |
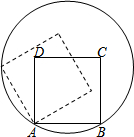 如图,已知正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点逆时针旋转,使点D落在⊙O上.若正方形ABCD的边长和⊙O的半径均为6cm,则点D运动的路径长为πcm.
如图,已知正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点逆时针旋转,使点D落在⊙O上.若正方形ABCD的边长和⊙O的半径均为6cm,则点D运动的路径长为πcm.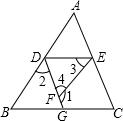 完成下面的证明.
完成下面的证明.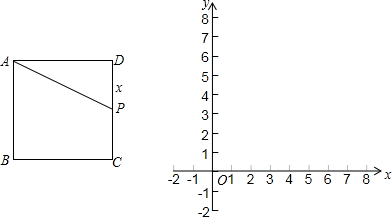
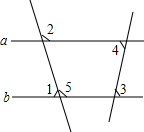 如图,已知∠1=80°,∠2=100°,∠3=85°,求∠4的度数.
如图,已知∠1=80°,∠2=100°,∠3=85°,求∠4的度数.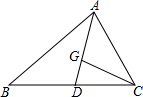 如图,在△ABC中,G是重心,点D是BC的中点,若△ABC的面积为6cm2,则△CGD的面积为1cm2.
如图,在△ABC中,G是重心,点D是BC的中点,若△ABC的面积为6cm2,则△CGD的面积为1cm2.